题目内容
已知非负实数x,y满足x+y=1,则
+
的最小值为( )
| 1 |
| x+1 |
| 4 |
| y+1 |
| A、1 | B、2 | C、3 | D、4 |
分析:将条件x+y=1转化为
[(x+1)+(y+1)]=1然后利用基本不等式的解法即可求出最小值.
| 1 |
| 3 |
解答:解:∵x+y=1,
∴x+1+y+1=3,
即
[(x+1)+(y+1)]=1,
∵非负实数x,y,
∴x+1>0,y+1>0,
∴
+
=(
+
)•
[(x+1)+(y+1)]=
[1+4+
+
]≥
[5+2
]=
?(5+4)=
=3,
当且仅当
=
,
即y+1=2(x+1)时取等号,
即x=0,y=1时取等号,
∴
+
的最小值为3.
故选:C.
∴x+1+y+1=3,
即
| 1 |
| 3 |
∵非负实数x,y,
∴x+1>0,y+1>0,
∴
| 1 |
| x+1 |
| 4 |
| y+1 |
| 1 |
| x+1 |
| 4 |
| y+1 |
| 1 |
| 3 |
| 1 |
| 3 |
| y+1 |
| x+1 |
| 4(x+1) |
| y+1 |
| 1 |
| 3 |
|
| 1 |
| 3 |
| 9 |
| 3 |
当且仅当
| y+1 |
| x+1 |
| 4(x+1) |
| y+1 |
即y+1=2(x+1)时取等号,
即x=0,y=1时取等号,
∴
| 1 |
| x+1 |
| 4 |
| y+1 |
故选:C.
点评:本题主要有考查基本不等式的应用,将条件x+y=1转化为
[(x+1)+(y+1)]=1是解决本题的关键,注意基本不等式成立的条件.
| 1 |
| 3 |

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
已知非负实数a,b满足2a+3b=10,则
+
最大值是( )
| 3b |
| 2a |
A、
| ||
B、2
| ||
| C、5 | ||
| D、10 |
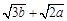 最大值是 ( )
最大值是 ( )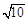 B.
B.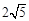 C.5 D.10
C.5 D.10 最大值是( )
最大值是( )
