题目内容
已知函数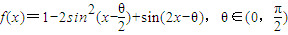 是定义在R 上的奇函数.
是定义在R 上的奇函数.(1)求θ的值和函数f(x)的单调递减区间;
(2)若三角形ABC三个内角A、B、C的对应边分别为a、b、c,△ABC的面积等于函数f(A)的最大值,求f(A)取最大值时a的最小值.
【答案】分析:(1)首先化简函数f(x),根据奇函数可知f(0)=0,以及θ的范围求出θ的值;由正弦函数的单调减区间,求得f(x)的单调减区间;
(2)先利用正弦的值域求得f(A)≤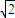 ,当A=
,当A=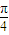 时等于三角形的面积,然后根据S△ABC=
时等于三角形的面积,然后根据S△ABC= ,求得bc=4,进而由余弦定理和放缩求得a 的最小值.
,求得bc=4,进而由余弦定理和放缩求得a 的最小值.
解答:解:(1)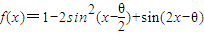 =
=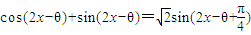 (2分)
(2分)
∵函数f(x)是定义在R上的奇函数,∴f(-x)=-f(x),易知f(0)=0,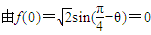 ,∴
,∴ ,∵
,∵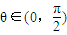 ,∴
,∴ ,∴
,∴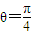 .(4分)
.(4分)
此时 为R上的奇函数,∴
为R上的奇函数,∴ 符合题意(5分)
符合题意(5分)
又由 ,得
,得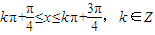 ,
,
∴函数f(x)的单调递减区间为 (7分)
(7分)
(2) ,
,
∴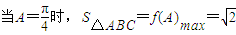 ,(9分)
,(9分) ,∴bc=4,(10分)
,∴bc=4,(10分)
由余弦定理可以知道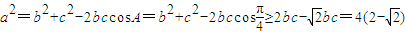 ,(12分)
,(12分)
∴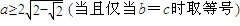 .
.
∴a的最小值是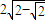 (14分)
(14分)
点评:本题考查了三角函数的最值和单调性,对于(2)问,注意放缩和余弦定理的运用,本题综合性强,属于中档题.
(2)先利用正弦的值域求得f(A)≤
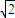 ,当A=
,当A=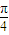 时等于三角形的面积,然后根据S△ABC=
时等于三角形的面积,然后根据S△ABC= ,求得bc=4,进而由余弦定理和放缩求得a 的最小值.
,求得bc=4,进而由余弦定理和放缩求得a 的最小值.解答:解:(1)
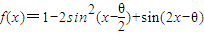 =
=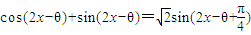 (2分)
(2分)∵函数f(x)是定义在R上的奇函数,∴f(-x)=-f(x),易知f(0)=0,
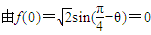 ,∴
,∴ ,∵
,∵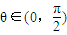 ,∴
,∴ ,∴
,∴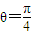 .(4分)
.(4分)此时
 为R上的奇函数,∴
为R上的奇函数,∴ 符合题意(5分)
符合题意(5分)又由
 ,得
,得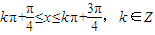 ,
,∴函数f(x)的单调递减区间为
 (7分)
(7分)(2)
 ,
,∴
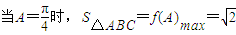 ,(9分)
,(9分) ,∴bc=4,(10分)
,∴bc=4,(10分)由余弦定理可以知道
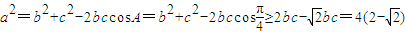 ,(12分)
,(12分)∴
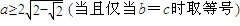 .
.∴a的最小值是
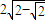 (14分)
(14分)点评:本题考查了三角函数的最值和单调性,对于(2)问,注意放缩和余弦定理的运用,本题综合性强,属于中档题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
 是定义在R上的奇函数,若对于任意给
是定义在R上的奇函数,若对于任意给 、
、 ,不等式
,不等式
 的解集为( ※ )
的解集为( ※ )



 是定义在R上的奇函数,
是定义在R上的奇函数, ,
,
 ,
, 的解集是 .
的解集是 .  是定义在R上的奇函数,当
是定义在R上的奇函数,当 时,
时, 则函数
则函数 =
= 在
在 上的所有零点之和为
上的所有零点之和为