题目内容
已知函数是定义在R上的偶函数,已知x≥0时,f(x)=-x+1,则f(x)的解析式为分析:由已知可以设x<0,然后利用函数的奇偶性转化到-x>0,利用已知求出x<0时的解析式即可.本题要做出整体代换,用-x代换x,然后写出整个定义域上的函数的解析式.
解答:解:设x<0,则-x>0,且有f(x)=f(-x)=-(-x)+1=x+1,
于是在定义域R上的函数f(x)的解析式为:
f(x)=
故答案为:f(x)=
于是在定义域R上的函数f(x)的解析式为:
f(x)=
|
故答案为:f(x)=
|
点评:本题考查函数的奇偶性,函数的解析式的求法,分段函数的概念,解析式以及性质的知识.

练习册系列答案
相关题目

 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当 时不等式
时不等式 成立, 若
成立, 若 ,
,
 ,则
,则 的大小关系是 .
的大小关系是 . 是定义在R上的增函数,且
是定义在R上的增函数,且 ,则m的取值范围是
.
,则m的取值范围是
. 是定义在R上的奇函数,
是定义在R上的奇函数, ,
,
 ,
,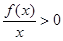 的解集是
.
的解集是
.