题目内容
已知函数是定义在R上的奇函数，当x＞0时，f（x）=x2-x，则f（-3）=（ ）
分析：利用函数的奇偶性将f（-3）转化为f（-3）=-f（3），然后直接代入解析式即可．
解答：解：∵函数f（x）是定义在R上的奇函数，
∴f（-3）=-f（3），
∵x＞0时，f（x）=x2-x，
∴f（-3）=-f（3）=-（9-3）=-6．
故选D．
∴f（-3）=-f（3），
∵x＞0时，f（x）=x2-x，
∴f（-3）=-f（3）=-（9-3）=-6．
故选D．
点评：本题主要考查函数奇偶性的应用，利用函数的奇偶性将f（-3）转化到已知条件上是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
是定义在R上的奇函数，且当
时不等式
成立， 若
，
，则
的大小关系是 ．
是定义在R上的增函数，且
，则m的取值范围是
.
是定义在R上的奇函数，
，
，
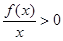的解集是
.