题目内容
如图,P是椭圆
+
=1(xy≠0)上的动点,F1、F2是椭圆的焦点,M是∠F1PF2的平分线上一点,且
•
=0.则|OM|的取值范围______.

| x2 |
| 25 |
| y2 |
| 16 |
| F2M |
| MP |

∵
•
=0,∴
⊥
延长F2M交PF1于点N,可知△PNF2为等腰三角形,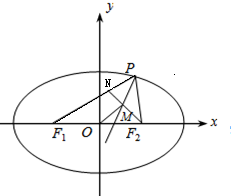
且M为F2M的中点,可得OM是△PF1F2的中位线
∴|OM|=
|NF1|=
(|PF1|-|PN|)
=
(|PF1|-|PF2|)=
(2a-2|PF2|)=a-|PF2|
∵a-c<|PF2|<a+c
∴0<|OM|<c=
=3
∴|OM|的取值范围是(0,3)
故答案为:(0,3)
| F2M |
| MP |
| F2M |
| MP |
延长F2M交PF1于点N,可知△PNF2为等腰三角形,

且M为F2M的中点,可得OM是△PF1F2的中位线
∴|OM|=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
∵a-c<|PF2|<a+c
∴0<|OM|<c=
| a2-b2 |
∴|OM|的取值范围是(0,3)
故答案为:(0,3)

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目