题目内容
在数列{an}中,a1=1,当n∈N*时,an+1=(
+1)an.数列{an}的前n项和为Sn,则
=______.
| 1 |
| n |
| lim |
| n→∞ |
| S2n |
| Sn |
∵a1=1,当n∈N*时,an+1=(
+1)an,
∴a2=2a1=2,
a3=
a2=3,
a4=
a3=4,
…
∴an=n,
∴Sn=1+2+3+…+n=
,
S2n=1+2+3+…+2n=
,
∴
=
=4.
故答案为:4.
| 1 |
| n |
∴a2=2a1=2,
a3=
| 3 |
| 2 |
a4=
| 4 |
| 3 |
…
∴an=n,
∴Sn=1+2+3+…+n=
| n(n+1) |
| 2 |
S2n=1+2+3+…+2n=
| 2n(2n+1) |
| 2 |
∴
| lim |
| n→∞ |
| S2n |
| Sn |
| lim |
| n→∞ |
| ||
|
故答案为:4.

练习册系列答案
相关题目
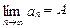 ,那么数列在区间
,那么数列在区间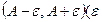 为任意小的正数)外的项有( )
为任意小的正数)外的项有( )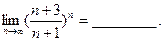
 = 。
= 。
