题目内容
数列{an}，通项公式为an=n2+an，若此数列为递增数列，则a的取值范围是（ ）
| A．a≥-2 | B．a＞-3 | C．a≤-2 | D．a＜0 |
∵an=n2+an，
∴an+1=（n+1）2+a（n+1）
∵an是递增数列，
∴（n+1）2+a（n+1）-n2-an＞0
化简可得2n+1+a＞0
∴a＞-2n-1，对于任意正整数n都成立，
∴a＞-3
故选B
∴an+1=（n+1）2+a（n+1）
∵an是递增数列，
∴（n+1）2+a（n+1）-n2-an＞0
化简可得2n+1+a＞0
∴a＞-2n-1，对于任意正整数n都成立，
∴a＞-3
故选B
练习册系列答案
相关题目
，
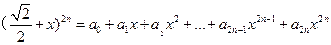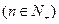，则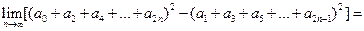
（ ）