题目内容
如图，直二面角D—AB—E中，四边形ABCD是边长为2的正方形，AE=EB，F为CE上的点，且BF⊥平面ACE.
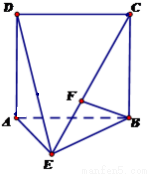
（Ⅰ）求证：AE⊥平面BCE；
（Ⅱ）求点D到平面ACE的距离。
【答案】
（Ⅰ）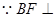
平面ACE.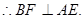 
∵二面角D—AB—E为直二面角，且
， 
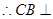平面ABE.
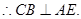
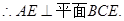
（Ⅱ）过点E作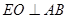
交AB于点O. OE=1.
∵二面角D—AB—E为直二面角，∴EO⊥平面ABCD.
设D到平面ACE的距离为h，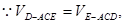
平面BCE，
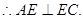
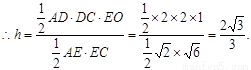
∴点D到平面ACE的距离为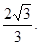
【解析】略
练习册系列答案
相关题目
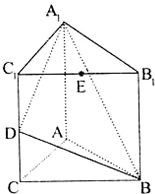直三棱柱A1B1C1-ABC的三视图如图所示，D、E分别为棱CC1和B1C1的中点．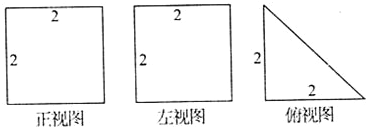
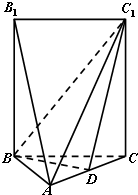如图，五面体A-BCC1B1中，AB1=4．底面ABC 是正三角形，AB=2．四边形BCC1B1是矩形，二面角A-BC-C1为直二面角．
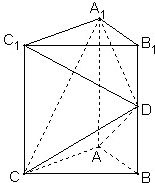如图，直三棱柱ABC-A1B1C1中，
如图：五面体A-BCC1B1中，AB1=4，△ABC 是正三角形，AB=2，四边形 BCC1B1是矩形，二面角A-BC-C1为直二面角，D为AC的中点．
如图，直四棱柱A1B1C1D1-ABCD的高为3，底面是边长为4，且∠DAB=60°的菱形，O是AC与BD的交点，O1是A1C1与B1D1的交点．