题目内容
15.定义在R上的偶函数f(x)满足f(x+1)=-f(x),且当x∈[-1,0)时f(x)=($\frac{1}{2}$)x,则 f(log28)等于( )| A. | 3 | B. | $\frac{1}{8}$ | C. | -2 | D. | 2 |
分析 由函数f(x)满足f(x+1)=-f(x),变形得到函数的周期,然后利用函数的周期性把f(log28)转化为求给出的函数解析式范围内的值,从而得到答案.
解答 解:由f(x+1)=f(x-1),
则偶函数f(x)为周期为2的周期函数,
∴f(log28)=f(3log22)=f(3)=f(3-2)=f(1)=f(-1).
又当x∈[-1,0]时f(x)=($\frac{1}{2}$)x,
∴f(log28)=f(-1)=($\frac{1}{2}$)-1=2.
故选:D
点评 本题考查了函数的周期性,考查了函数奇偶性的性质,考查了学生灵活分析问题和解决问题的能力,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.已知P(2,-3)是角θ终边上一点,则tan(2π+θ)等于( )
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | -$\frac{2}{3}$ |
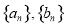 的前
的前 项和为分别是
项和为分别是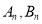 ,且
,且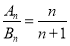 ,则
,则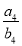 等于( )
等于( )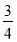 B.
B. C.
C. D.
D.