题目内容
(本小题满分13分)设函数f(x)=x3+ax2-a2x+m(a>0).
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若函数f(x)在x∈[-1,1]内没有极值点,求a的取值范围;
(Ⅲ)若对任意的a∈[ 3,6],不等式f(x)≤1在x∈[-2,2]上恒成立,求m的取值范围.
3,6],不等式f(x)≤1在x∈[-2,2]上恒成立,求m的取值范围.
解:(Ⅰ)∵f′(x)=3x2+2ax-a2=3(x-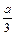 )(x+a)
)(x+a)
又a>0,∴当x<-a或x>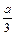 时f′(x)>0;
时f′(x)>0;
当-a<x<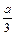 时,f′(x)<0.
时,f′(x)<0.
∴函数f(x)的单调递增区间为(-∞,-a),(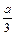 ,+∞),
,+∞),
单调递减区间为(-a,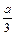 ).(4分)
).(4分)
(Ⅱ)由题设可知,方程f′(x)=3x2+2ax-a2=0在[-1,1]上没有实根
∴ ,解得a>3. (8分)
,解得a>3. (8分)
(Ⅲ)∵a∈[3,6],∴由(Ⅰ)知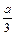 ∈[1,2],-a≤-3
∈[1,2],-a≤-3
又x∈[-2,2]
∴f(x)max=max{f(-2),f(2)}
而f(2)-f(-2)=16-4a2<0
∴f(x)max=f(-2)=-8+4a+2a2+m (10分)又∵f(x)≤1在[-2,2]上恒成立
∴f(x)max≤1即-8+4a+2a2+m≤1
即m≤9-4a- 2a2,在a∈[3,6]上恒成立
2a2,在a∈[3,6]上恒成立
∵9-4a-2a2的最小值为-87
∴m≤-87.  (13分)
(13分)
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
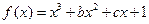 的单调减区间是(1,2)
的单调减区间是(1,2)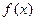 的解析式;
的解析式;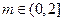 ,关于
,关于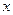 的不等式
的不等式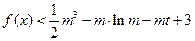 在
在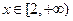 时有解,求实数
时有解,求实数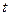 的取值范围.
的取值范围. ,2]都有|f(x)|≤1
,2]都有|f(x)|≤1 .
. 在区间[-3,4]
在区间[-3,4] 上的值域
上的值域 ,直线
,直线 ,直线
,直线
 (其中
(其中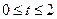 ,
, 为常数);.若直线
为常数);.若直线 1、
1、 的图象以及
的图象以及 、
、 轴与函数
轴与函数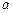 、
、 、
、 的值;
的值; 关于
关于 的解析式;
的解析式; 问是否存在实数
问是否存在实数 ,使得
,使得 的图象与
的图象与 的图象有且只有两个不同的交点?若存在,求出
的图象有且只有两个不同的交点?若存在,求出
 ,
, ,
, 在(0,4)上为单调函数,求
在(0,4)上为单调函数,求 的取值范围.
的取值范围.
 的单调区间;
的单调区间;
 ,在(1,2)上为单调递
,在(1,2)上为单调递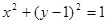 的圆心到直线
的圆心到直线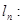
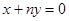 (
(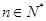 )的距离为
)的距离为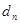 ,则
,则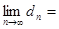 .
. 的图象过点
的图象过点 ,且在
,且在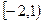 内
内 上单
上单 调递增.
调递增.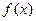 的解析式;
的解析式; ,不等式
,不等式 恒成立,试问
恒成立,试问 是否存在.若存在,请求出
是否存在.若存在,请求出