题目内容
【题目】已知正四棱锥P﹣ABCD如图.
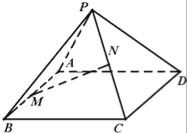
(Ⅰ)若其正视图是一个边长分别为![]() 、
、![]() ,2的等腰三角形,求其表面积S、体积V;
,2的等腰三角形,求其表面积S、体积V;
(Ⅱ)设AB中点为M,PC中点为N,证明:MN∥平面PAD.
【答案】(Ⅰ)![]() (Ⅱ)详见解析
(Ⅱ)详见解析
【解析】
试题分析:(I)作出棱锥的高和斜高,利用勾股定理求出棱锥的高,代入面积,体积公式计算;(II)取PD的中点Q,证明AMNQ是平行四边形得出MN∥AQ,于是MN∥平面PAD
试题解析:(I)过P作PE⊥CD于E,过P作PO⊥平面ABCD,垂足为O,
则PE⊥CD,E为CD的中点,O为正方形ABCD的中心.
∵正四棱锥的正视图是一个边长分别为![]() 、
、![]() ,2的等腰三角形,
,2的等腰三角形,
∴PE=![]() ,BC=CD=2,
,BC=CD=2,
∴OE=![]() ,∴PO=
,∴PO=![]() =
=![]() .
.
∴正四棱锥的表面积S=S正方形ABCD+4S△PCD=22+4×![]() =4+4
=4+4![]() .
.
正四棱锥的体积V=![]() =
=![]() =
=![]() .
.
(II)过N作NQ∥CD,连结AQ,
∵N为PC的中点,∴Q为PD的中点,
∴NQ![]()
![]() CD,又AM
CD,又AM![]()
![]() CD,
CD,
∴AM![]() NQ,
NQ,
∴四边形AMNQ是平行四边形,
∴MN∥AQ,又MN平面PAD,AQ平面PAD,
∴MN∥平面PAD.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
【题目】为了参加市高中篮球比赛,某中学决定从四个篮球较强的班级的篮球队员中选出![]() 人组成男子篮球队,代表该地区参赛,四个篮球较强的班级篮球队员人数如下表:
人组成男子篮球队,代表该地区参赛,四个篮球较强的班级篮球队员人数如下表:
班级 | 高三(7)班 | 高三(17)班 | 高二(31)班 | 高二(32)班 |
人数 | 12 | 6 | 9 | 9 |
(1)现采取分层抽样的方法从这四个班中抽取运动员,求应分别从这四个班抽出的队员人数;
(2)该中学篮球队奋力拼搏,获得冠军.若要从高三年级抽出的队员中选出两位队员作为冠军的代表发言,求选出的两名队员来自同一班的概率.