题目内容
(2011•福建模拟)给出以下四个结论:
(1)若关于x的方程x-
+k=0在x∈(0,1)没有实数根,则k的取值范围是k≥2
(2)曲线y=1+
(|x|≤2)与直线y=k(x-2)+4有两个交点时,实数k的取值范围是(
,
]
(3)已知点P(a,b)与点Q(1,0)在直线2x-3y+1=0两侧,则3b-2a>1;
(4)若将函数f(x)=sin(2x-
)的图象向右平移?(?>0)个单位后变为偶函数,则?的最小值是
,其中正确的结论是:
(1)若关于x的方程x-
| 1 |
| x |
(2)曲线y=1+
| 4-x2 |
| 5 |
| 12 |
| 3 |
| 4 |
(3)已知点P(a,b)与点Q(1,0)在直线2x-3y+1=0两侧,则3b-2a>1;
(4)若将函数f(x)=sin(2x-
| π |
| 3 |
| π |
| 12 |
(2)(3)(4)
(2)(3)(4)
.分析:根据方程根与函数零点的关系,利用图象法,易判断(1)的真假;先确定曲线的性质,然后结合图形确定临界状态,结合直线与圆相交的性质,可解得k的取值范围,从而判断(2)的真假.根据平面点与直线的位置关系,可以求出a,b满足的不等式,可判断(3)的真假;根据正弦型函数的对称性,及函数图象的平移变换,可判断(4)的真假,进而得到答案.
解答:解:(1)若关于x的方程 x-
+k=0在x∈(0,1)没有实数根,则k的取值范围是k≤0,故(2)错误;
对于(2),y=1+
可化为x2+(y-1)2=4,y≥1,所以曲线为以(0,1)为圆心,2为半径的圆y≥1的部分.
直线y=k(x-2)+4过定点p(2,4),由图知,当直线经过A(-2,1)点时恰与曲线有两个交点,顺时针旋转到与曲线相切时交点边为一个.
且kAP=
=
,由直线与圆相切得d=
=2,解得k=
则实数k的取值范围为 (
,
],故正确;
对于(3),点P(a,b)与点Q(1,0)在直线2x-3y+1=0两侧,则2a-3b+1<0,故(3)正确;
(4)若将函数 f(x)=sin(2x-
)的图象向右平移?(?>0)个单位后变为偶函数,则φ=kπ+
,k∈N,当k=0时,?的最小值是
,故(4)正确;
故答案为:(2)、(3)、(4).
| 1 |
| x |
对于(2),y=1+
| 4-x2 |

直线y=k(x-2)+4过定点p(2,4),由图知,当直线经过A(-2,1)点时恰与曲线有两个交点,顺时针旋转到与曲线相切时交点边为一个.
且kAP=
| 4-1 |
| 2+2 |
| 3 |
| 4 |
| |-1+4-2k| | ||
|
| 5 |
| 12 |
则实数k的取值范围为 (
| 5 |
| 12 |
| 3 |
| 4 |
对于(3),点P(a,b)与点Q(1,0)在直线2x-3y+1=0两侧,则2a-3b+1<0,故(3)正确;
(4)若将函数 f(x)=sin(2x-
| π |
| 3 |
| π |
| 12 |
| π |
| 12 |
故答案为:(2)、(3)、(4).
点评:本题考查的知识点是函数图象的平移变换,函数的值域,简单线性规划的应用,直线与圆相交的性质等,其中熟练掌握相应基础知识点的熟练应用是解答本题的关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
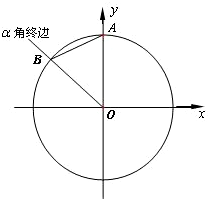 (2011•福建模拟)如图,单位圆(半径为1的圆)的圆心O为坐标原点,单位圆与y轴的正半轴交与点A,与钝角α的终边OB交于点B(xB,yB),设∠BAO=β.
(2011•福建模拟)如图,单位圆(半径为1的圆)的圆心O为坐标原点,单位圆与y轴的正半轴交与点A,与钝角α的终边OB交于点B(xB,yB),设∠BAO=β.