题目内容
(2011•福建模拟)如图1,在直角梯形ABCD中,AB∥CD,AB⊥AD,且AB=AD=
CD=1.
现以AD为一边向形外作正方形ADEF,然后沿边AD将正方形ADEF翻折,使平面ADEF与平面ABCD垂直,M为ED的中点,如图2.
(1)求证:AM∥平面BEC;
(2)求证:BC⊥平面BDE;
(3)求三棱锥D-BCE的体积.

| 1 | 2 |
现以AD为一边向形外作正方形ADEF,然后沿边AD将正方形ADEF翻折,使平面ADEF与平面ABCD垂直,M为ED的中点,如图2.
(1)求证:AM∥平面BEC;
(2)求证:BC⊥平面BDE;
(3)求三棱锥D-BCE的体积.

分析:(1)取EC中点N,连接MN,BN,证明BN∥AM.说明BN?平面BEC,且AM?平面BEC,即可证明AM∥平面BEC;
(2)先证明ED⊥BC,BC⊥BD,ED∩BD=D,即可证明BC⊥平面BDE;
(3)利用VE-BCD=VD-BCE,求出底面DCB的面积,高DE,即可求三棱锥D-BCE的体积.
(2)先证明ED⊥BC,BC⊥BD,ED∩BD=D,即可证明BC⊥平面BDE;
(3)利用VE-BCD=VD-BCE,求出底面DCB的面积,高DE,即可求三棱锥D-BCE的体积.
解答:解: (1)证明:取EC中点N,M是EC的中点,连接MN,BN.
(1)证明:取EC中点N,M是EC的中点,连接MN,BN.
在△EDC中,M,N分别为ED,EC的中点,
所以MN∥CD,且MN=
CD.
由已知AB∥CD,AB=
CD,
所以MN∥AB,且MN=AB. (3分)
所以四边形ABNM为平行四边形.
所以BN∥AM. (4分)
又因为BN?平面BEC,且AM?平面BEC,
所以AM∥平面BEC. (4分)
(2)证明:在正方形ADEF中,ED⊥AD.
又因为平面ADEF⊥平面ABCD,且平面ADEF∩平面ABCD=AD,
所以ED⊥平面ABCD.
所以ED⊥BC. (6分)
在直角梯形ABCD中,AB=AD=1,CD=2,可得BC=
.
在△BCD中,BD=BC=
,CD=2,所以BD2+BC2=CD2.
所以BC⊥BD.
所以BC⊥平面BDE. (8分)
(3)由(2)知,BC⊥BE,BC⊥BD
所以S△BCD=
BD•BC=
•
•
=1,又因为ED⊥平面ABCD,DE=1
∴VE-BCD=VD-BCE=
S△BCD•DE=
•(12分)
 (1)证明:取EC中点N,M是EC的中点,连接MN,BN.
(1)证明:取EC中点N,M是EC的中点,连接MN,BN.在△EDC中,M,N分别为ED,EC的中点,
所以MN∥CD,且MN=
| 1 |
| 2 |
由已知AB∥CD,AB=
| 1 |
| 2 |
所以MN∥AB,且MN=AB. (3分)
所以四边形ABNM为平行四边形.
所以BN∥AM. (4分)
又因为BN?平面BEC,且AM?平面BEC,
所以AM∥平面BEC. (4分)
(2)证明:在正方形ADEF中,ED⊥AD.
又因为平面ADEF⊥平面ABCD,且平面ADEF∩平面ABCD=AD,
所以ED⊥平面ABCD.
所以ED⊥BC. (6分)
在直角梯形ABCD中,AB=AD=1,CD=2,可得BC=
| 2 |
在△BCD中,BD=BC=
| 2 |
所以BC⊥BD.
所以BC⊥平面BDE. (8分)
(3)由(2)知,BC⊥BE,BC⊥BD
所以S△BCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
∴VE-BCD=VD-BCE=
| 1 |
| 3 |
| 1 |
| 3 |
点评:本题是中档题,考查直线与平面的平行与垂直的证明方法,几何体的体积的解法,考查空间想象能力、计算能力,注意转化思想的应用,判定定理的正确应用.

练习册系列答案
相关题目
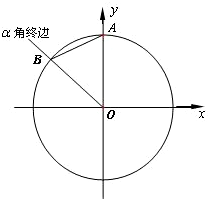 (2011•福建模拟)如图,单位圆(半径为1的圆)的圆心O为坐标原点,单位圆与y轴的正半轴交与点A,与钝角α的终边OB交于点B(xB,yB),设∠BAO=β.
(2011•福建模拟)如图,单位圆(半径为1的圆)的圆心O为坐标原点,单位圆与y轴的正半轴交与点A,与钝角α的终边OB交于点B(xB,yB),设∠BAO=β.