题目内容
(2011•福建模拟)已知函数f(x)=2x-2lnx
(Ⅰ)求函数在(1,f(1))的切线方程
(Ⅱ)求函数f(x)的极值
(Ⅲ)对于曲线上的不同两点P1(x1,y1),P2(x2,y2),如果存在曲线上的点Q(x0,y0),且x1<x0<x2,使得曲线在点Q处的切线l∥P1P2,则称l为弦P1P2的陪伴切线.已知两点A(1,f(1)),B(e,f(e)),试求弦AB的陪伴切线l的方程.
(Ⅰ)求函数在(1,f(1))的切线方程
(Ⅱ)求函数f(x)的极值
(Ⅲ)对于曲线上的不同两点P1(x1,y1),P2(x2,y2),如果存在曲线上的点Q(x0,y0),且x1<x0<x2,使得曲线在点Q处的切线l∥P1P2,则称l为弦P1P2的陪伴切线.已知两点A(1,f(1)),B(e,f(e)),试求弦AB的陪伴切线l的方程.
分析:(I)利用切线的斜率是函数在切点处导数,求出切线斜率,再利用直线方程的点斜式求出切线方程.
(II)首先对函数求导,使得导函数等于0,解出x的值,分两种情况讨论:当f′(x)>0,即x>1;当f′(x)<0,即0<x<1时,列表做出函数的极值点,求出极值.
(III)设出切点坐标,根据坐标表示出切线的斜率,然后把切点的横坐标代入到曲线的导函数中得到切线的斜率,根据伴随切线的含义写出弦AB的伴随切线l的方程即可.
(II)首先对函数求导,使得导函数等于0,解出x的值,分两种情况讨论:当f′(x)>0,即x>1;当f′(x)<0,即0<x<1时,列表做出函数的极值点,求出极值.
(III)设出切点坐标,根据坐标表示出切线的斜率,然后把切点的横坐标代入到曲线的导函数中得到切线的斜率,根据伴随切线的含义写出弦AB的伴随切线l的方程即可.
解答:解:(I)∵y=2x-2lnx,∴y′=2-2×
∴函数y=2x-2lnx在x=1处的切线斜率为0,
又∵切点坐标为(1,2)
切线方程为y=2;
(Ⅱ)f′(x)=2-
,x>0.…(6分)
f′(x)=0,得x=1.
当x变化时,f′(x)与f(x)变化情况如下表:
∴当x=1时,f(x)取得极小值f(1)=2. 没有极大值. …(9分)
(Ⅲ)设切点Q(x0,y0),则切线l的斜率为f′(x0)=2-
,x0∈(1,e).
弦AB的斜率为kAB=
=
=2-
. …(10分)
由已知得,l∥AB,则2-
=2-
,解得x0=e-1,代入函数式得y0=2(e-1)-2ln(e-1)
解出切点坐标(e-1,2(e-1)-2ln(e-1))…(12分)
再由点斜式写出方程y-2(e-1)+2ln(e-1)=
(x-e-1),即:y=
x+2-2ln(e-1),
所以,弦AB的伴随切线l的方程为:y=
x+2-2ln(e-1).…(13分)
| 1 |
| x |
∴函数y=2x-2lnx在x=1处的切线斜率为0,
又∵切点坐标为(1,2)
切线方程为y=2;
(Ⅱ)f′(x)=2-
| 2 |
| x |
f′(x)=0,得x=1.
当x变化时,f′(x)与f(x)变化情况如下表:
| x | (0,1) | 1 | (1,+∞) |
| f′(x) | - | 0 | + |
| f(x) | 单调递减 | 极小值 | 单调递增 |
(Ⅲ)设切点Q(x0,y0),则切线l的斜率为f′(x0)=2-
| 2 |
| x0 |
弦AB的斜率为kAB=
| f(e)-f(1) |
| e-1 |
| 2(e-1)-2(1-0) |
| e-1 |
| 2 |
| e-1 |
由已知得,l∥AB,则2-
| 2 |
| x0 |
| 2 |
| e-1 |
解出切点坐标(e-1,2(e-1)-2ln(e-1))…(12分)
再由点斜式写出方程y-2(e-1)+2ln(e-1)=
| 2e-4 |
| e-1 |
| 2e-4 |
| e-1 |
所以,弦AB的伴随切线l的方程为:y=
| 2e-4 |
| e-1 |
点评:本题考查利用导数研究曲线上某点切线方程、函数极值的求法,本题解题的关键是对函数求导,求出导函数等于0时对应的变量的取值,再进行讨论,本题是一个中档题目,这个知识点一般出现在综合题目中.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
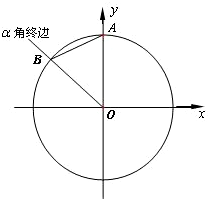 (2011•福建模拟)如图,单位圆(半径为1的圆)的圆心O为坐标原点,单位圆与y轴的正半轴交与点A,与钝角α的终边OB交于点B(xB,yB),设∠BAO=β.
(2011•福建模拟)如图,单位圆(半径为1的圆)的圆心O为坐标原点,单位圆与y轴的正半轴交与点A,与钝角α的终边OB交于点B(xB,yB),设∠BAO=β.