题目内容
已知函数f（x）是定义在[-5，5]上的偶函数，且f（x）在[0，5]上的图象如图所示，其中满足f（0）=0，f（5）=2，最高点为（2，5），（1）试将函数f（x）在[-5，5]的图象补充完整；
（2）写出f（x）的单调区间（无需证明）；
（3）若方程f（x）=m有两个解，写出所有满足条件的m值构成的集合M．
分析：（1）根据函数奇偶性的对称性即可将函数f（x）在[-5，5]的图象补充完整；
（2）根据函数图象和单调性之间的关系即可写出f（x）的单调区间；
（3）根据函数图象即可得得到方程f（x）=m解得情况．
（2）根据函数图象和单调性之间的关系即可写出f（x）的单调区间；
（3）根据函数图象即可得得到方程f（x）=m解得情况．
解答：解（1）∵函数f（x）是定义在[-5，5]上的偶函数，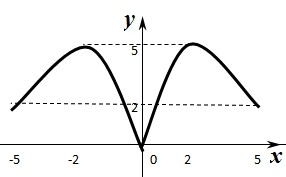
∴函数图象关于y轴对称，
∴对应的图象如右图：
（2）由图象可知函数的增区间[-5，-2]，[0，2]．
减区间[-2，0]，[2，5]．
（3）由图象可知，要使方程f（x）=m有两个解，
则0＜m＜2或m=5，
即集合M={m|0＜m＜2或m=5}．
∴函数图象关于y轴对称，
∴对应的图象如右图：
（2）由图象可知函数的增区间[-5，-2]，[0，2]．
减区间[-2，0]，[2，5]．
（3）由图象可知，要使方程f（x）=m有两个解，
则0＜m＜2或m=5，
即集合M={m|0＜m＜2或m=5}．
点评：本题主要考查函数奇偶性和单调性的判断，利用数形结合是解决本题的关键，比较基础．
练习册系列答案
天天练口算系列答案
相关题目
已知函数f（x）=x+