题目内容
已知动点P到直线x=-1的距离与到定点C(
, 0)的距离的差为
.动点P的轨迹设为曲线C.
(Ⅰ)求曲线C的方程;
(Ⅱ)设过点A(-4,0)的直线与曲线C交于E、F两点,定点A'(4,0),求直线A'E、A'F的斜率之和.
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅰ)求曲线C的方程;
(Ⅱ)设过点A(-4,0)的直线与曲线C交于E、F两点,定点A'(4,0),求直线A'E、A'F的斜率之和.
分析:(Ⅰ)由题意知,动点P到定点C(
, 0)的距离等于到定直线x=-
的距离,所以动点P的轨迹为抛物线,由此能求出点P的轨迹方程.
(Ⅱ)设过点A的直线方程为y=k(x+4)(k≠0).联立方程组
,得
y2-y+4k=0,由此能够求出直线A′E、A′F的斜率之和.
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)设过点A的直线方程为y=k(x+4)(k≠0).联立方程组
|
| k |
| 2 |
解答:解:(Ⅰ)由题意知,动点P到定点C(
, 0)的距离等于到定直线x=-
的距离,
所以动点P的轨迹为抛物线,
且
=
,
P=1.
所以点P的轨迹方程为y2=2x.…(6分)
(Ⅱ)设过点A的直线方程为y=k(x+4)(k≠0).
联立方程组
,
消去x,得
y2-y+4k=0.…(8分)
设E(x1,y1)、F(x2,y2),
则y1•y2=8,且y12=2x1,y22=2x2.
∵kA′E=
,kA′F=
,
∴kA′E+kA′F=
+
=
=
=
.
由y1•y2=8,得kA'E+kA'F=0.…(14分)
| 1 |
| 2 |
| 1 |
| 2 |
所以动点P的轨迹为抛物线,
且
| p |
| 2 |
| 1 |
| 2 |
P=1.
所以点P的轨迹方程为y2=2x.…(6分)
(Ⅱ)设过点A的直线方程为y=k(x+4)(k≠0).
联立方程组
|
消去x,得
| k |
| 2 |
设E(x1,y1)、F(x2,y2),
则y1•y2=8,且y12=2x1,y22=2x2.
∵kA′E=
| y1 |
| x1-4 |
| y2 |
| x2-4 |
∴kA′E+kA′F=
| y1 |
| x1-4 |
| y2 |
| x2-4 |
| y1x2-4y1+y2x1-4y2 |
| (x1-4)(x2-4) |
=
y1
| ||||||||
| (x1-4)(x2-4) |
=
(y1+y2)(
| ||||
| (x1-4)(x2-4) |
由y1•y2=8,得kA'E+kA'F=0.…(14分)
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与抛物线的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
相关题目
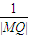 ,
,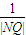 )都在以原点为圆心,定值r为半径的圆上?若存在,求出m、n、r的值;若不存在,说明理由.
)都在以原点为圆心,定值r为半径的圆上?若存在,求出m、n、r的值;若不存在,说明理由.