题目内容
已知动点P到直线x=2的距离等于P到圆x2-7x+y2+4=0的切线长,设点P的轨迹为曲线E;
(1)求曲线E的方程;
(2)是否存在一点Q(m,n),过点Q任作一直线与轨迹E交于M、N两点,点 (
,
)都在以原点为圆心,定值r为半径的圆上?若存在,求出m、n、r的值;若不存在,说明理由.
(1)求曲线E的方程;
(2)是否存在一点Q(m,n),过点Q任作一直线与轨迹E交于M、N两点,点 (
| 1 |
| |MQ| |
| 1 |
| |NQ| |
分析:(1)设P(x,y),由题意可得,|x-2|=
整理可得切线E的方程
(2)过点Q任作的直线方程可设为:
(α为直线的倾斜角),代入曲线E的方程y2=3x,得(n+tsinα)2=3(m+tcosα),sin2αt2+(2nsinα-3cosα)t+n2-3m=0,由韦达定理得t1+t2=
,t1t2=
,若使得点 (
,
)在以原点为圆心,定值r为半径的圆上,则有
+
=
+
=
=
=
为定值
(x-
|
(2)过点Q任作的直线方程可设为:
|
| 3cosα-2nsinα |
| sin2α |
| n2-3m |
| sin2α |
| 1 |
| |MQ| |
| 1 |
| |NQ| |
| 1 |
| |MQ|2 |
| 1 |
| |NQ|2 |
| 1 |
| t12 |
| 1 |
| t22 |
| t12+t22 |
| (t1t2)2 |
| (t1+t2)2-2t1t2 |
| (t1t2)2 |
| 9-12nsinαcosα+(2n2+6m-9)sin2α |
| (n2-3m)2 |
解答:解:(1)设P(x,y),圆方程x2-7x+y2+4=0化为标准式:(x-
)2+y2=
则有|x-2|=
∴(x-2)2=x2-7x+y2+4,整理可得y2=3x
∴曲线E的方程为y2=3x.
(2)过点Q任作的直线方程可设为:
(α为直线的倾斜角)
代入曲线E的方程y2=3x,得(n+tsinα)2=3(m+tcosα),sin2αt2+(2nsinα-3cosα)t+n2-3m=0
由韦达定理得t1+t2=
,t1t2=
,
+
=
+
=
=
=
=
=
═
令-12n与2n2+6m-9同时为0
得n=0,m=
,此时
+
=
为定值r=
故存在.
| 7 |
| 2 |
| 33 |
| 4 |
则有|x-2|=
(x-
|
∴(x-2)2=x2-7x+y2+4,整理可得y2=3x
∴曲线E的方程为y2=3x.
(2)过点Q任作的直线方程可设为:
|
代入曲线E的方程y2=3x,得(n+tsinα)2=3(m+tcosα),sin2αt2+(2nsinα-3cosα)t+n2-3m=0
由韦达定理得t1+t2=
| 3cosα-2nsinα |
| sin2α |
| n2-3m |
| sin2α |
| 1 |
| |MQ|2 |
| 1 |
| |NQ|2 |
| 1 |
| t12 |
| 1 |
| t22 |
| t12+t22 |
| (t1t2)2 |
| (t1+t2)2-2t1t2 |
| (t1t2)2 |
(
| ||||
(
|
| (3cosα-2nsinα)2-2(n2-3m)sin2α |
| (n2-3m)2 |
| 9cos2α-12nsinαcosα+2n2sin2α+6msin2α |
| (n2-3m)2 |
| 9-12nsinαcosα+(2n2+6m-9)sin2α |
| (n2-3m)2 |
令-12n与2n2+6m-9同时为0
得n=0,m=
| 3 |
| 2 |
| 1 |
| |MQ|2 |
| 1 |
| |NQ|2 |
| 4 |
| 9 |
| 2 |
| 3 |
点评:本题主要考查了点到直线的距离公式得应用,直线的参数方程的应用,直线与曲线相交的位置关系及方程思想的应用,解题要求具备一定得推理与运算得能力

练习册系列答案
相关题目
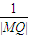 ,
,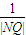 )都在以原点为圆心,定值r为半径的圆上?若存在,求出m、n、r的值;若不存在,说明理由.
)都在以原点为圆心,定值r为半径的圆上?若存在,求出m、n、r的值;若不存在,说明理由.