题目内容
已知动点P到直线x=4的距离等于到定点F1(1,0)的距离的2倍,
(1)求动点P的轨迹方程;
(2)过F1且斜率k=1的直线交上述轨迹于C、D两点,若A(2,0),求△ACD的面积S.
(1)求动点P的轨迹方程;
(2)过F1且斜率k=1的直线交上述轨迹于C、D两点,若A(2,0),求△ACD的面积S.
分析:(1)将已知条件动点P到直线x=4的距离等于到定点F1(1,0)的距离的2倍,用坐标表示为|x-4|=2
,化简得到动点P(x,y)的轨迹方程.
(2)写出直线的方程,将直线方程代入椭圆的方程,利用韦达定理得到|y1-y2|,利用三角形的面积公式S△ACD=
|AF1|•|y1-y2|求出△ACD的面积S.
| (x-1)2+y2 |
(2)写出直线的方程,将直线方程代入椭圆的方程,利用韦达定理得到|y1-y2|,利用三角形的面积公式S△ACD=
| 1 |
| 2 |
解答:解:(1)设动点P(x,y),由题设知|x-4|=2
,
化简得动点P(x,y)的轨迹方程是
+
=1.
(2)过F1(1,0)且斜率k=1的直线方程为y=x-1代入椭圆方程消去y,
得 7x2-8x-8=0.
设C(x1,y1),D(x2,y2),
则|y1-y2|=|x1-x2|=
=
而S△ACD=
|AF1|•|y1-y2|=
×1×
=
| (x-1)2+y2 |
化简得动点P(x,y)的轨迹方程是
| x2 |
| 4 |
| y2 |
| 3 |
(2)过F1(1,0)且斜率k=1的直线方程为y=x-1代入椭圆方程消去y,
得 7x2-8x-8=0.
设C(x1,y1),D(x2,y2),
则|y1-y2|=|x1-x2|=
| (x1+x2)2-4x1x2 |
12
| ||
| 7 |
而S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
12
| ||
| 7 |
6
| ||
| 7 |
点评:解决直线与圆锥曲线的位置关系问题,一般思路是将直线的方程与圆锥曲线的方程联立,消去一个未知数,利用韦达定理找突破口.

练习册系列答案
相关题目
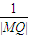 ,
,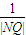 )都在以原点为圆心,定值r为半径的圆上?若存在,求出m、n、r的值;若不存在,说明理由.
)都在以原点为圆心,定值r为半径的圆上?若存在,求出m、n、r的值;若不存在,说明理由.