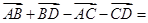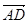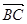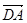题目内容
在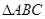 中,已知
中,已知 =1,则
=1,则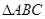 面积的最大值是 。
面积的最大值是 。
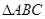 中,已知
中,已知 =1,则
=1,则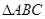 面积的最大值是 。
面积的最大值是 。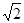
因为∴1=AB2AC2cos2A(1)又∵S=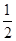 |AB||AC|sinA∴4S2=AB2AC2sin2A(2)(1)+(2)得:1+4S2=AB2AC2(cos2A+sin2A)即1+4S2=AB2AC2
|AB||AC|sinA∴4S2=AB2AC2sin2A(2)(1)+(2)得:1+4S2=AB2AC2(cos2A+sin2A)即1+4S2=AB2AC2
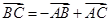
∴BC2=AC2-2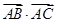 +AB2=AC2+AB2-2∵BC=2,
+AB2=AC2+AB2-2∵BC=2,
∴AC2+AB2=6由不等式:AC2+AB2≥2AC•AB 当且仅当,AC=AB时,取等号∴6≥2AC•AB即AC•AB≤3∴1+4S2=AB2AC2《9∴4S2≤8,即:S2≤2,故则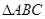 面积的最大值是
面积的最大值是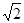
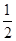 |AB||AC|sinA∴4S2=AB2AC2sin2A(2)(1)+(2)得:1+4S2=AB2AC2(cos2A+sin2A)即1+4S2=AB2AC2
|AB||AC|sinA∴4S2=AB2AC2sin2A(2)(1)+(2)得:1+4S2=AB2AC2(cos2A+sin2A)即1+4S2=AB2AC2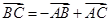
∴BC2=AC2-2
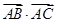 +AB2=AC2+AB2-2∵BC=2,
+AB2=AC2+AB2-2∵BC=2,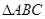 面积的最大值是
面积的最大值是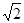

练习册系列答案
相关题目
 外一点,若
外一点,若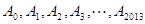 中任意相邻两点的距离相等,
中任意相邻两点的距离相等,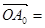 a,
a,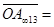 b用a,b表示
b用a,b表示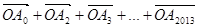 其结果为( )
其结果为( )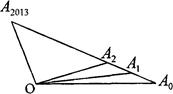
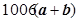


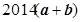
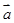 ,
,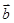 ,
,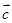 为任意非零向量,且相互不共线,则以下结论正确的为
为任意非零向量,且相互不共线,则以下结论正确的为 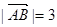 ,
, ,则
,则 +
+
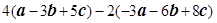 =__________.
=__________.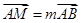 ,
,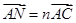 ,则
,则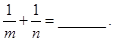
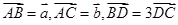 ,用
,用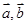 表示
表示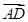 ,则
,则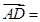

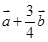
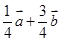
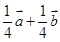
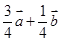
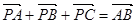 ,则下列结论正确的是( )
,则下列结论正确的是( )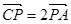 B.P在AB上,且
B.P在AB上,且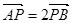
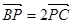 D.P点为△的重心
D.P点为△的重心