题目内容
12.函数$f(x)=\sqrt{x+2}+\frac{2}{3-x}$的定义域为[-2,3)∪(3,+∞).分析 由根式内部的代数式大于等于0,分式的分母不为0求得x的取值集合得答案.
解答 解:由$\left\{\begin{array}{l}{x+2≥0}\\{3-x≠0}\end{array}\right.$,解得x≥-2且x≠3.
∴函数$f(x)=\sqrt{x+2}+\frac{2}{3-x}$的定义域为[-2,3)∪(3,+∞).
故答案为:[-2,3)∪(3,+∞).
点评 本题考查函数的定义域及其求法,是基础题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
2.圆O:x2+y2+4x=0的圆心O坐标和半径r分别是( )
| A. | O (-2,0),r=2 | B. | O(-2,0),r=4 | C. | O(2,0),r=2 | D. | O(2,0),r=4 |
20.设0<a<1,在下列四个不等式中,正确的是( )
| A. | (1-a)a>(1+a)a | B. | log1-a(1+a)<0 | C. | (1-a)1+a>1 | D. | ${(1-a)}^{\frac{1}{a}}$>1 |
7.已知α=20°,则tanα+4sinα的值为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
 已知函数f(x)=2sin(ωx+φ)其中x∈R,ω>0,-π<φ<π)的部分图象如图所示,则函数f(x)的解析式是$f(x)=2sin(2x+\frac{2π}{3})$.
已知函数f(x)=2sin(ωx+φ)其中x∈R,ω>0,-π<φ<π)的部分图象如图所示,则函数f(x)的解析式是$f(x)=2sin(2x+\frac{2π}{3})$.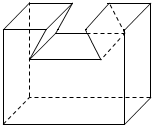 如图中的组合体的结构特征有以下几种说法:
如图中的组合体的结构特征有以下几种说法: 如图,△PBD是直角三角形,∠PDB=90°,以BA为直径作⊙O,设点C是圆⊙O与直线PD的公共点,若∠ABC=∠DBC.
如图,△PBD是直角三角形,∠PDB=90°,以BA为直径作⊙O,设点C是圆⊙O与直线PD的公共点,若∠ABC=∠DBC.