题目内容
7.已知α=20°,则tanα+4sinα的值为( )| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
分析 由条件利用同角三角函数的基本关系,两角差的三角公式化简所给的式子,求得结果.
解答 解:α=20°,则tanα+4sinα=$\frac{sin20°+4sin20°cos20°}{cos20°}$=$\frac{sin20°+2sin40°}{cos20°}$=$\frac{sin(60°-40°)+2sin40°}{cos(60°-40°)}$
=$\frac{\frac{\sqrt{3}}{2}cos40°+\frac{3}{2}sin40°}{\frac{1}{2}cos40°+\frac{\sqrt{3}}{2}sin40°}$=$\sqrt{3}$,
故选:B.
点评 本题主要考查同角三角函数的基本关系,两角差的三角公式,属于基础题.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
18.下列各组中的函数图象相同的是( )
| A. | f(x)=1,g(x)=x0 | B. | f(x)=1,g(x)=$\frac{x}{x}$ | ||
| C. | f(x)=$\frac{(x+3)^{2}}{x+3}$,g(x)=(x+3)(x+3)0 | D. | f(x)=|x|,g(x)=$\left\{\begin{array}{l}{x,x>0}\\{-x,x<0}\end{array}\right.$ |
17.f(x)=3x+3x-8,则函数f(x)的零点落在区间( )参考数据:31.25≈3.9,31.5≈5.2.
| A. | (1,1.25) | B. | (1.25,1.5) | C. | (1.5,2) | D. | 不能确定 |
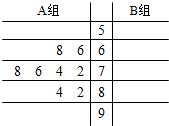 某班A、B两组各有8名学生,他们期中考试的美术成绩如下:
某班A、B两组各有8名学生,他们期中考试的美术成绩如下: 在等腰梯形ABCD中,AB∥CD,AB=BC=AD=2,CD=4,E为边DC的中点.如图1.将△ADE沿AE折起到△AEP位置,连PB、PC,点Q是棱AE的中点,点M在棱PC上,如图2.
在等腰梯形ABCD中,AB∥CD,AB=BC=AD=2,CD=4,E为边DC的中点.如图1.将△ADE沿AE折起到△AEP位置,连PB、PC,点Q是棱AE的中点,点M在棱PC上,如图2.