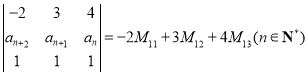题目内容
【题目】设函数![]() ,
,![]() a为实数
a为实数![]() ,
,
![]() 求函数
求函数![]() 的单调区间;
的单调区间;
![]() 若存在实数a,使得
若存在实数a,使得![]() 对任意
对任意![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.![]() 提示:
提示:![]()
【答案】(1)![]() 单调递减,
单调递减,![]() 单调递增;(2)
单调递增;(2)![]()
【解析】
(1)求出![]() ,在定义域内,分别令
,在定义域内,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间,![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(2)令
的减区间;(2)令![]() ,
,![]() 时,不合题意,
时,不合题意,![]() 时,利用导数求得
时,利用导数求得![]() ,问题等价于
,问题等价于![]() 恒成立,再利用导数求得
恒成立,再利用导数求得![]() 的最大值即可得结果.
的最大值即可得结果.
(1)![]() ,
,
由![]() ,得
,得![]() ,
,
![]() ,得
,得![]() ,
,
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(2)令![]() ,
,
则![]() ,
,
若e-a≥0,可得h′(x)>0,函数h(x)为增函数,当x→+∞时,h(x)→+∞,
不满足h(x)≤0对任意x∈R恒成立;
若e-a<0,由h’(x)=0,得![]() ,则
,则![]() ,
,
∴当x∈![]() 时,h′(x)>0,当x∈
时,h′(x)>0,当x∈![]() 时,h′(x)<0,
时,h′(x)<0,
∴![]() ,
,
若f(x)≤g(x)对任意x∈R恒成立, 则![]() ≤0(a>e)恒成立,
≤0(a>e)恒成立,
若存在实数a,使得![]() ≤0成立, 则ma≥
≤0成立, 则ma≥![]() ,
,
∴![]() (a>e),
(a>e),
令F(a)![]() , 则
, 则![]() .
.
∴当a<2e时,F′(a)<0,当a>2e时,F′(a)>0,
则![]() .
.
∴m![]() . 则实数m的取值范围是
. 则实数m的取值范围是![]() .
.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目