题目内容
【题目】如图，直线l⊥平面α，垂足为O，已知△ABC中，∠ABC为直角，AB=2，BC=1，该直角三角形做符合以下条件的自由运动：（1）A∈l，（2）B∈α．则C、O两点间的最大距离为 ．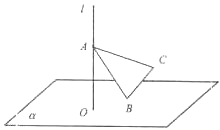 
【答案】
【解析】解：将原问题转化为平面内的最大距离问题解决，
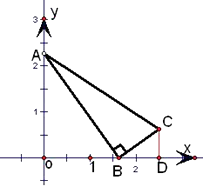
以O为原点，OA为y轴，OB为x轴建立直角坐标系，如图．
设∠ABO=θ，C（x，y），则有：
x=ABcosθ+BCsinθ
=2cosθ+sinθ，
y=BCcosθ
=cosθ．
∴x2+y2=4cos2θ+4sinθcosθ+1
=2cos2θ+2sin2θ+3
=2 
sin（2θ+ 
）+3，
当sin（2θ+ ）=1时，x2+y2最大，为2 +3，
则C、O两点间的最大距离为
所以答案是： ．
练习册系列答案
相关题目
