题目内容
【题目】函数y=log 
（﹣3+4x﹣x2）的单调递增区间是（ ）
A.（﹣∞，2）
B.（2，+∞）
C.（1，2）
D.（2，3）
【答案】D
【解析】解：由﹣3+4x﹣x2＞0得x2﹣4x+3＜0，得1＜x＜3，
设t=﹣3+4x﹣x2 ， 则对称轴为x=2，
则函数y=log 
t为减函数，
则要求函数y=log （﹣3+4x﹣x2）的单调递增区间，
即求函数t=﹣3+4x﹣x2的单调递减区间，
∵函数t=﹣3+4x﹣x2的单调递减区间是（2，3），
∴函数y=log （﹣3+4x﹣x2）的单调递增区间为（2，3），
故选：D．
【考点精析】关于本题考查的复合函数单调性的判断方法，需要了解复合函数f[g(x)]的单调性与构成它的函数u=g(x)，y=f(u)的单调性密切相关，其规律：“同增异减”才能得出正确答案．
练习册系列答案
阅读快车系列答案
相关题目
【题目】如表提供了甲产品的产量x（吨）与利润y（万元）的几组对照数据．
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
（1）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程 
= 
x+ 
；
（2）计算相关指数R2的值，并判断线性模型拟合的效果．
参考公式： = 
= 
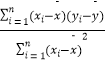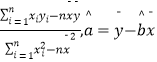，R2=1﹣ 
．
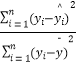