题目内容
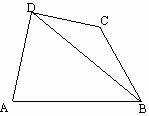
如图，在四边形ABCD中，已知AD^CD, AD=10, AB=14, ÐBDA=60°, ÐBCD=135° 求BC的长．
解：在△ABD中，设BD=x
则
即142=x2+102-2.10xcos600
整理得：x2-10x-96=0
解之：x1=16 ,x2=-6（舍去）
由正弦定理：
∴BC=16sin300/sin1350=8
答：略。
练习册系列答案
相关题目
题目内容
如图，在四边形ABCD中，已知AD^CD, AD=10, AB=14, ÐBDA=60°, ÐBCD=135° 求BC的长．
解：在△ABD中，设BD=x
则
即142=x2+102-2.10xcos600
整理得：x2-10x-96=0
解之：x1=16 ,x2=-6（舍去）
由正弦定理：
∴BC=16sin300/sin1350=8
答：略。
如图，在四边形ABCD中，△ABC为边长等于
如图，在四边形ABCD中，AC平分∠DAB，∠ABC=60°，AC=7，AD=6，S△ADC=
如图，在四边形ABCD中，AC平分∠DAB，∠ABC=60°，AC=6，AD=5，S△ADC=
如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，过点B作射线BBl∥AC．动点D从点A出发沿射线AC方向以每秒5个单位的速度运动，同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动．过点D作DH⊥AB于H，过点E作EF⊥AC交射线BB1于F，G是EF中点，连接DG．设点D运动的时间为t秒．
（2012•青岛二模）如图，在多面体ABC-A1B1C1中，四边形ABB1A1是正方形，AC=AB=1，A1C=A1B，B1C1∥BC，