题目内容
【题目】已知函数f(x)=log2(1+x)﹣log2(1﹣x),g(x)=log2(1+x)+log2(1﹣x).
(1)判断函数f(x)奇偶性并证明;
(2)判断函数f(x)单调性并用单调性定义证明;
(3)求函数g(x)的值域.
【答案】
(1)解:由 ![]() 得
得 ![]() ,即﹣1<x<1,即函数的定义域为(﹣1,1),关于原点对称
,即﹣1<x<1,即函数的定义域为(﹣1,1),关于原点对称
f(﹣x)=﹣f(x)∴f(x)为(﹣1,1)上的奇函数
(2)解:设﹣1<x1<x2<1,
则 ![]() =
= ![]() ,
,
又﹣1<x1<x2<1∴(1+x1)(1﹣x2)﹣(1﹣x1)(1+x2)=2(x1﹣x2)<0
即0<(1+x1)(1﹣x2)<(1﹣x1)(1+x2),
∴ ![]() ,
,
∴ ![]() ,
,
∴f(x1)<f(x2),
∴f(x)在(﹣1,1)上单调递增
(3)解:由 ![]() 得
得 ![]() ,即﹣1<x<1,即函数的定义域为(﹣1,1),
,即﹣1<x<1,即函数的定义域为(﹣1,1),
则g(x)=log2(1+x)+log2(1﹣x)=g(x)=log2[(1+x)(1﹣x)]=log2(1﹣x2)≤log21=0,
即g(x)的值域为(﹣∞,0]
【解析】(1)根据函数奇偶性的定义即可判断函数f(x)奇偶性并证明;(2)根据函数单调性的定义即可判断函数f(x)单调性并用单调性定义证明;(3)根据函数奇偶性和单调性的关系即可求函数g(x)的值域.
【考点精析】本题主要考查了奇偶性与单调性的综合的相关知识点,需要掌握奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性才能正确解答此题.

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案【题目】为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有800名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩进行统计. 请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
分组 | 频数 | 频率 |
50.5~60.5 | 6 | 0.08 |
60.5~70.5 | 0.16 | |
70.5~80.5 | 15 | |
80.5~90.5 | 24 | 0.32 |
90.5~100.5 | ||
合计 | 75 | 1.00 |
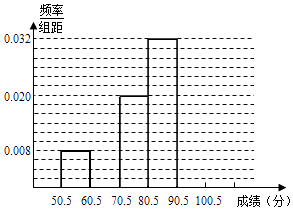
(1)填充频率分布表的空格;
(2)补全频率分布直方图;
(3)根据频率分布直方图求此次“环保知识竞赛”的平均分为多少?
