题目内容
(本题满分12分)已知函数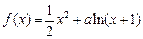 .
.
(Ⅰ)当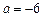 时,求函数
时,求函数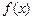 的单调区间和极值;
的单调区间和极值;
(Ⅱ)若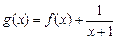 在
在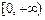 上是单调递增函数,求实数
上是单调递增函数,求实数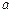 的取值范围.
的取值范围.
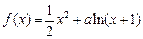 .
.(Ⅰ)当
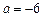 时,求函数
时,求函数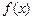 的单调区间和极值;
的单调区间和极值; (Ⅱ)若
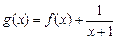 在
在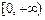 上是单调递增函数,求实数
上是单调递增函数,求实数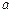 的取值范围.
的取值范围.(Ⅰ)
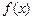 的单调递减区间为
的单调递减区间为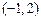 ,单调递增区间为
,单调递增区间为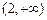 ,
,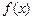 在
在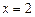 处取到极小值,且
处取到极小值,且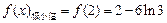 ,
,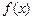 无极大值.
无极大值. (Ⅱ)
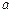 ≥1
≥1解:(Ⅰ)当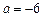 时,
时,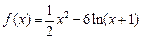 ,定义域满足:
,定义域满足: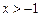
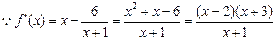 ,且
,且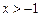 …… 2分
…… 2分
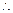 当
当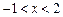 时,
时,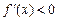 ,当
,当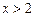 时,
时,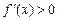 …… 3分
…… 3分
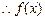 的单调递减区间为
的单调递减区间为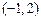 ,单调递增区间为
,单调递增区间为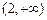 , …… 4分
, …… 4分
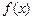 在
在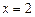 处取到极小值,且
处取到极小值,且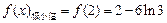 …… 5分
…… 5分
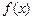 无极大值. …… 6分
无极大值. …… 6分
(Ⅱ)由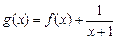 =
=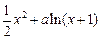
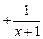
得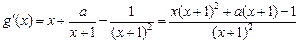 …… 7分
…… 7分
由已知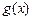 在
在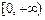 上是单调递增函数,
上是单调递增函数,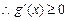 …… 8分
…… 8分
即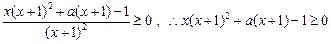
整理得: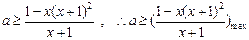 …… 9分
…… 9分
令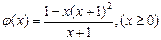 ,则由
,则由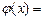
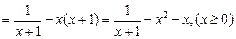
得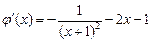 …… 10分
…… 10分
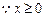 ,
,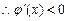 ,
,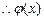 在
在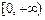 上是单调递减函数, …… 11分
上是单调递减函数, …… 11分
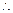 当
当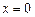 时,得
时,得 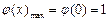
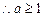 ……12分
……12分
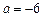 时,
时,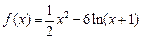 ,定义域满足:
,定义域满足: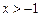
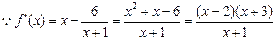 ,且
,且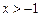 …… 2分
…… 2分 当
当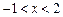 时,
时,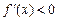 ,当
,当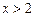 时,
时,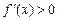 …… 3分
…… 3分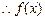 的单调递减区间为
的单调递减区间为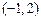 ,单调递增区间为
,单调递增区间为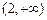 , …… 4分
, …… 4分
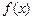 在
在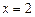 处取到极小值,且
处取到极小值,且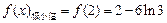 …… 5分
…… 5分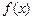 无极大值. …… 6分
无极大值. …… 6分(Ⅱ)由
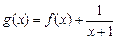 =
=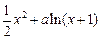
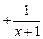
得
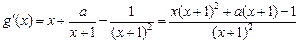 …… 7分
…… 7分由已知
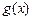 在
在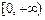 上是单调递增函数,
上是单调递增函数,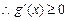 …… 8分
…… 8分即
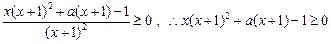
整理得:
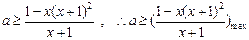 …… 9分
…… 9分令
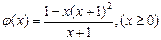 ,则由
,则由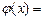
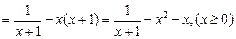
得
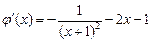 …… 10分
…… 10分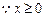 ,
,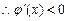 ,
,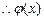 在
在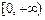 上是单调递减函数, …… 11分
上是单调递减函数, …… 11分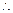 当
当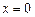 时,得
时,得 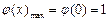
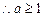 ……12分
……12分
练习册系列答案
相关题目
 的任意实数
的任意实数 ,使得不等式
,使得不等式 恒成立,
恒成立, 的取值范围.
的取值范围.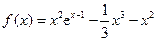 设
设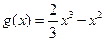 ,试比较
,试比较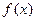 与
与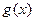 的大小
的大小
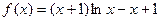 .
.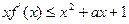 ,求a的取值范围;
,求a的取值范围;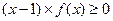 .
.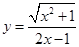 的导数是 ( )
的导数是 ( )



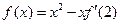 ,则
,则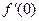 等于
等于  (2)
(2)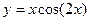
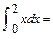 ____________
____________