题目内容
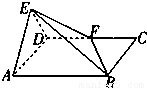
如图,平面EAD⊥平面ABFD,△AED为正三角形,四边形ABFD为直角梯形,且∠BAD=90°,AB∥DF,AD=a,AB=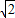 a,DF=
a,DF=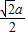 .
. (I)求证:EF⊥FB;
(II)求直线EB和平面ABFD所成的角.

【答案】分析:(I)过点E向AD引垂线交AD于点O,根据△AED为正三角形以及平面EAD⊥平面ABFD可得EO⊥平面ABFD;先连接OF,求出OF,BF,OB的平方,得到OF⊥FB;再结合EO⊥FB,证得FB⊥平面EOF即可得到EF⊥FB;
(II)根据(I)得EO⊥平面ABFD,可得直线EB和平面ABCD所成的角为∠EBO.再RT△EOB中求出任意两边长即可求直线EB和平面ABFD所成的角.
解答: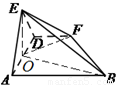 解:(I)过点E向AD引垂线交AD于点O,根据△AED为正三角形以及平面EAD⊥平面ABFD
解:(I)过点E向AD引垂线交AD于点O,根据△AED为正三角形以及平面EAD⊥平面ABFD
可得EO⊥平面ABFD
连接OF,则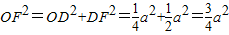 ,
, ,
,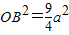 ,
,
所以OB2=OF2+FB2,即OF⊥FB. ①
又因为EO⊥平面ABFD
所以EO⊥FB,②
所以FB⊥平面EOF,得EF⊥FB.(5分)
(II)由(I)得,EO⊥平面ABFD,
则直线EB和平面ABCD所成的角为∠EBO.
因为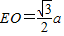 ,
,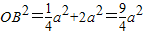 ,得
,得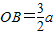 ,
,
所以 ,即
,即 .(10分)
.(10分)
点评:本题主要考查直线与平面垂直、直线与平面所成的角等基础知识,考查空间想象能力、运算能力、推理论证能力.
(II)根据(I)得EO⊥平面ABFD,可得直线EB和平面ABCD所成的角为∠EBO.再RT△EOB中求出任意两边长即可求直线EB和平面ABFD所成的角.
解答:
 解:(I)过点E向AD引垂线交AD于点O,根据△AED为正三角形以及平面EAD⊥平面ABFD
解:(I)过点E向AD引垂线交AD于点O,根据△AED为正三角形以及平面EAD⊥平面ABFD可得EO⊥平面ABFD
连接OF,则
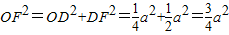 ,
, ,
,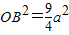 ,
,所以OB2=OF2+FB2,即OF⊥FB. ①
又因为EO⊥平面ABFD
所以EO⊥FB,②
所以FB⊥平面EOF,得EF⊥FB.(5分)
(II)由(I)得,EO⊥平面ABFD,
则直线EB和平面ABCD所成的角为∠EBO.
因为
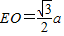 ,
,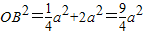 ,得
,得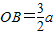 ,
,所以
 ,即
,即 .(10分)
.(10分)点评:本题主要考查直线与平面垂直、直线与平面所成的角等基础知识,考查空间想象能力、运算能力、推理论证能力.

练习册系列答案
相关题目
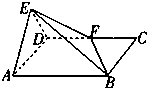 如图,平面EAD⊥平面ABCD,△EAD为正三角形,四边形ABCD为矩形,F是CD中点,EB与平面ABCD成30°角.
如图,平面EAD⊥平面ABCD,△EAD为正三角形,四边形ABCD为矩形,F是CD中点,EB与平面ABCD成30°角. 如图,在三棱锥A-BCD中,DA,DB,DC两两垂直,且长度均为1,E为BC中点,则下列结论正确的是( )
如图,在三棱锥A-BCD中,DA,DB,DC两两垂直,且长度均为1,E为BC中点,则下列结论正确的是( ) 如图,平面EAD⊥平面ABFD,△AED为正三角形,四边形ABFD为直角梯形,且∠BAD=90°,
如图,平面EAD⊥平面ABFD,△AED为正三角形,四边形ABFD为直角梯形,且∠BAD=90°, 如图,平面EAD⊥平面ABFD,△AED为正三角形,四边形ABFD为直角梯形,且∠BAD=90°,AB∥DF,AD=a,AB=
如图,平面EAD⊥平面ABFD,△AED为正三角形,四边形ABFD为直角梯形,且∠BAD=90°,AB∥DF,AD=a,AB=