题目内容
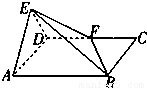
如图,平面EAD⊥平面ABCD,△EAD为正三角形,四边形ABCD为矩形,F是CD中点,EB与平面ABCD成30°角.(1)当AD长度为何值时,点A到平面EFB的距离为2?
(2)二面角A-BF-E的大小是否与AD的长度有关?请说明.
【答案】分析:(1)取AD的中点O,连接OE、OB,由,△EAD为正三角形,平面EAD⊥平面ABCD,由等腰三角形性质及线面垂直的性质,可得EO⊥平面ABCD,由EB与平面ABCD成30°角设AD=2a,则可以以O为坐标原点,建立空间坐标系,分别求出对应点的坐标,根据点A到平面EFB的距离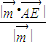 =2,构造关于a的方程,解方程即可求出AD长.
=2,构造关于a的方程,解方程即可求出AD长.
(2)结合(1)的结合,求出平面EFB与平面ABCD的法向量,代入向量夹角公式,即可求出答案.
解答:解:(1)取AD的中点O,连接OE、OB,
则EO⊥AD,EO⊥平面ABCD
于是∠EBO=30°
设AD=2a,则EO=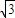 a,AB=2
a,AB=2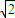 a,OB=3a
a,OB=3a
建立如图所示的直角坐标系,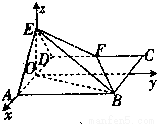
则a=(a,0,0),B(a,2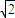 a,0),E=(0,0,
a,0),E=(0,0,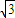 a),F(-a,
a),F(-a, a,0)
a,0)
∴ =(-a,
=(-a,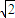 a,-
a,- a),
a), =(a,2
=(a,2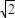 a,-
a,-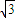 a),
a),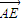 =(a,0,
=(a,0,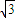 a),
a),
∴可求得平面EFB的法向量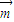 =(1,-
=(1,- ,-
,-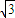 ),|
),| |=
|=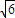
∴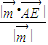 =2
=2
∴AD=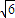 (6分)
(6分)
(2)平面ABCD的一个法向量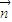 =(0,0,1)
=(0,0,1)
设二面角A-BF-E的大小为θ
则cosθ=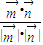 =
=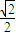
∴AD长度不影响二面角A-BF-E的大小 (12分)
点评:本题考查的知识点是二面角的平面角及求法,点到平面的距离计算,其中建立空间坐标系,利用向量法解答点到平面的距离及二面角问题是解答本题的关键.
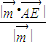 =2,构造关于a的方程,解方程即可求出AD长.
=2,构造关于a的方程,解方程即可求出AD长.(2)结合(1)的结合,求出平面EFB与平面ABCD的法向量,代入向量夹角公式,即可求出答案.
解答:解:(1)取AD的中点O,连接OE、OB,
则EO⊥AD,EO⊥平面ABCD
于是∠EBO=30°
设AD=2a,则EO=
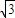 a,AB=2
a,AB=2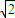 a,OB=3a
a,OB=3a建立如图所示的直角坐标系,

则a=(a,0,0),B(a,2
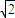 a,0),E=(0,0,
a,0),E=(0,0,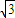 a),F(-a,
a),F(-a, a,0)
a,0)∴
 =(-a,
=(-a,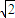 a,-
a,- a),
a), =(a,2
=(a,2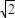 a,-
a,-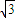 a),
a),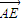 =(a,0,
=(a,0,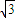 a),
a),∴可求得平面EFB的法向量
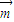 =(1,-
=(1,- ,-
,-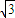 ),|
),| |=
|=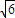
∴
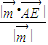 =2
=2∴AD=
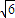 (6分)
(6分)(2)平面ABCD的一个法向量
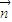 =(0,0,1)
=(0,0,1)设二面角A-BF-E的大小为θ
则cosθ=
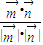 =
=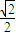
∴AD长度不影响二面角A-BF-E的大小 (12分)
点评:本题考查的知识点是二面角的平面角及求法,点到平面的距离计算,其中建立空间坐标系,利用向量法解答点到平面的距离及二面角问题是解答本题的关键.

练习册系列答案
相关题目
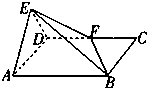 如图,平面EAD⊥平面ABCD,△EAD为正三角形,四边形ABCD为矩形,F是CD中点,EB与平面ABCD成30°角.
如图,平面EAD⊥平面ABCD,△EAD为正三角形,四边形ABCD为矩形,F是CD中点,EB与平面ABCD成30°角. 如图,在三棱锥A-BCD中,DA,DB,DC两两垂直,且长度均为1,E为BC中点,则下列结论正确的是( )
如图,在三棱锥A-BCD中,DA,DB,DC两两垂直,且长度均为1,E为BC中点,则下列结论正确的是( ) 如图,平面EAD⊥平面ABFD,△AED为正三角形,四边形ABFD为直角梯形,且∠BAD=90°,
如图,平面EAD⊥平面ABFD,△AED为正三角形,四边形ABFD为直角梯形,且∠BAD=90°, 如图,平面EAD⊥平面ABFD,△AED为正三角形,四边形ABFD为直角梯形,且∠BAD=90°,AB∥DF,AD=a,AB=
如图,平面EAD⊥平面ABFD,△AED为正三角形,四边形ABFD为直角梯形,且∠BAD=90°,AB∥DF,AD=a,AB=