题目内容
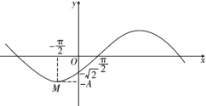
【题目】已知函数f(x)＝
x3－2x2＋3x(x∈R)的图象为曲线C.
(1)求过曲线C上任意一点切线斜率的取值范围；
(2)若在曲线C上存在两条相互垂直的切线，求其中一条切线与曲线C的切点的横坐标的取值范围．
【答案】（1）[－1，＋∞)；（2）(－∞，2－
]∪(1,3)∪[2＋
，＋∞).
【解析】试题分析：（1）先求导函数，然后根据导函数求出其取值范围，从而可求出曲线C上任意一点处的切线的斜率的取值范围；（2）根据（1）可知k与﹣
的取值范围，从而可求出k的取值范围，然后解不等式可求出曲线C的切点的横坐标取值范围.
解析：
(1)由题意得f′(x)＝x2－4x＋3，则f′(x)＝(x－2)2－1≥－1，
即过曲线C上任意一点切线斜率的取值范围是[－1，＋∞)．
(2)设曲线C的其中一条切线的斜率为k，则由(2)中条件并结合(1)中结论可知，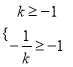 
解得－1≤k＜0或k≥1，故由－1≤x2－4x＋3＜0或x2－4x＋3≥1，
得x∈(－∞，2－
]∪(1,3)∪[2＋
，＋∞)
练习册系列答案
相关题目
【题目】企业需为员工缴纳社会保险，缴费标准是根据职工本人上一年度月平均工资（单位：元）的
缴纳，
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
t | 1 | 2 | 3 | 4 | 5 |
y | 270 | 330 | 390 | 460 | 550 |
某企业员工甲在2014年至2018年各年中每月所撒纳的养老保险数额y（单位：元）与年份序号t的统计如下表：
（1）求出t关于t的线性回归方程
；
（2）试预测2019年该员工的月平均工资为多少元？
附：回归直线的斜率和截距的最小二乘法估计公式分别为：
（注：
，
，其中
）