题目内容
函数y=log x+log2x2+2的值域是( )
x+log2x2+2的值域是( )
| A.(0,+∞) | B.[1,+∞) | C.(1,+∞) | D.R |
B
解析试题分析:因为y=log x+log2x2+2= y=log
x+log2x2+2= y=log x+2log2x+2,所以令t=
x+2log2x+2,所以令t= ,x>0,t
,x>0,t ,
,
有y=t +2t+2=(t+1)
+2t+2=(t+1) +1,函数值域为[1,+∞),选B。
+1,函数值域为[1,+∞),选B。
考点:本题主要考查对数函数的性质,二次函数的图象和性质。
点评:小综合题,将 看成一个变量,利用换元法再应用二次函数性质。
看成一个变量,利用换元法再应用二次函数性质。

练习册系列答案
相关题目
下列函数中,在区间 上为减函数的是( )
上为减函数的是( )
A. | B. | C. | D. |
若a是函数 的零点,若
的零点,若 ,则
,则 的值满足
的值满足
A. | B. | C. | D. 的符号不确定 的符号不确定 |
函数y= 的定义域为( )
的定义域为( )
A.(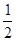 ,+∞) ,+∞) | B.[1,+∞ | C.( 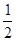 ,1 ,1 | D.(-∞,1)) |
设函数f (x)=x3-4x+a,0<a<2.若f (x)的三个零点为x1,x2,x3,且x1<x2<x3,则
| A.x1>-1 | B.x2<0 | C.x2>0 | D.x3>2 |
函数 在区间
在区间 单调递增,则实数
单调递增,则实数 的取值范围为
的取值范围为
A. | B. | C. | D. |
若方程 的根在区间
的根在区间 上,则
上,则 的值为( )
的值为( )
A. | B.1 |
C. 或2 或2 | D. 或1 或1 |
 的图象的大致形状是
的图象的大致形状是 
 ,则函数
,则函数 的图象大致为( )
的图象大致为( )