题目内容
已知直线 经过两点(2,1),(6,3)
经过两点(2,1),(6,3)
(1)求直线 的方程
的方程
(2)圆C的圆心在直线 上,并且与
上,并且与 轴相切于点(2,0), 求圆C的方程
轴相切于点(2,0), 求圆C的方程
(1)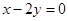 ;(2)
;(2)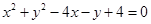
解析试题分析:(1)由直线的两点式方程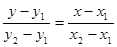 可直接得出,或者先由两点求其斜率,再用直线的点斜式方程
可直接得出,或者先由两点求其斜率,再用直线的点斜式方程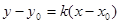 ;(2)求圆的方程 ,只需确定其圆心和半径,由题意可知,圆心横坐标是2,代入直线方程求其纵坐标,从而圆心确定,因为圆C与
;(2)求圆的方程 ,只需确定其圆心和半径,由题意可知,圆心横坐标是2,代入直线方程求其纵坐标,从而圆心确定,因为圆C与 轴相切,所以半径就是圆心的纵坐标的绝对值,从而圆的方程确定.
轴相切,所以半径就是圆心的纵坐标的绝对值,从而圆的方程确定.
试题解析:(1)由题可知:直线l经过点(2, 1), (6, 3),由两点式可得直线l的方程为: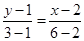 整理得:
整理得: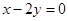 5分
5分
(2)依题意:设圆C的方程为: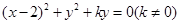 其圆心为
其圆心为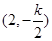
,∵圆心C在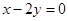 上,∴2-2·
上,∴2-2·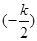 =0,
=0,
∴k=-1,∴圆C的方程为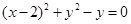
即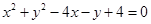 12分
12分
考点:1、直线的方程;2、圆的方程.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
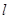 经过点
经过点 ,且斜率为
,且斜率为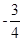 .
.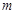 与
与 垂直;
垂直;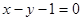 与
与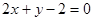 的交点,且平行于直线
的交点,且平行于直线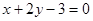 的直线方程.
的直线方程.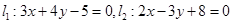 的交点M,且满足下列条件的直线方程:(1)与直线2x+3y+5=0平行; (2)与直线2x+3y+5=0垂直.
的交点M,且满足下列条件的直线方程:(1)与直线2x+3y+5=0平行; (2)与直线2x+3y+5=0垂直.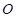 :
: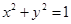 和定点
和定点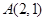 ,由⊙
,由⊙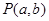 向⊙
向⊙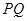 ,切点为
,切点为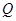 ,且满足
,且满足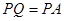 .
.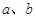 间满足的等量关系;
间满足的等量关系;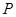 为圆心所作的⊙
为圆心所作的⊙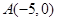 ,
,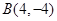 ,
,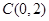 ,
,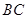 边上的中线所在直线方程;
边上的中线所在直线方程;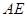 所在直线方程.
所在直线方程.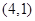 ,B
,B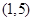 ,C
,C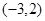 ;
;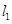 :
: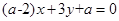 和
和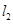 :
: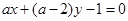 。
。