题目内容
求经过直线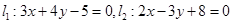 的交点M,且满足下列条件的直线方程:(1)与直线2x+3y+5=0平行; (2)与直线2x+3y+5=0垂直.
的交点M,且满足下列条件的直线方程:(1)与直线2x+3y+5=0平行; (2)与直线2x+3y+5=0垂直.
(1)2x+3y-4=0;(2)3x-2y+7=0.
解析试题分析:(1)与直线2x+3y+5=0平行的直线假设为2x+3y+c=0平行,代入交点坐标即可求出c的值.(2)与直线2x+3y+5=0垂直的直线假设为3x-2y+b=0,代入交点解出b的值即可.
试题解析:由题意知:两条直线的交点为(-1,2),
(1)因为过(-1,2),所以与2x+3y+5=0平行的直线为2x+3y-4=0.
(2)设与2x+3y+5=0垂直的直线方程为3x-2y+b=0,又过点(-1,2),代入得b=7,
故,直线方程为3x-2y+7=0
考点:1.平行直线间的关系.2.垂直直线间的关系.

练习册系列答案
相关题目
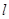 :
: 和
和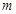 :
: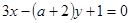 互相平行,求实数
互相平行,求实数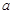 的值.
的值.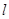 经过直线2x+y-2=0与x-2y+1=0的交点,且与直线
经过直线2x+y-2=0与x-2y+1=0的交点,且与直线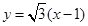 的夹角为
的夹角为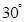 ,求直线
,求直线 的交点M,且满足下列条件的直线方程:
的交点M,且满足下列条件的直线方程: 经过两点(2,1),(6,3)
经过两点(2,1),(6,3) 轴相切于点(2,0), 求圆C的方程
轴相切于点(2,0), 求圆C的方程 中,已知圆
中,已知圆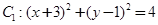 和圆
和圆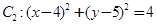 .
. 过点
过点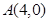 ,且被圆
,且被圆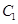 截得的弦长为
截得的弦长为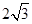 ,求直线
,求直线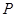 为平面上的点,满足:存在过点
为平面上的点,满足:存在过点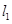 和
和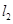 ,它们分别与圆
,它们分别与圆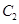 相交,且直线
相交,且直线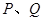 分别为曲线
分别为曲线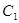 和
和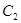 上的点,把
上的点,把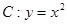 到直线
到直线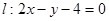 的距离;
的距离;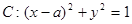 到直线
到直线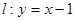 的距离为
的距离为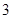 ,求实数
,求实数 的值;
的值;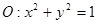 到曲线
到曲线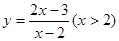 的距离.
的距离.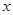 O
O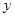 中,直线
中,直线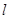 与抛物线
与抛物线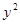 =2
=2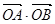 =3”是真命题;
=3”是真命题;