题目内容
设等差数列{an}的前n项和为Sn,已知a3=12,S12>0,S13<0.
(1)求公差d的取值范围;
(2)指出S1、S2、…、S12中哪一个值最大,并说明理由.
(1) 公差d的取值范围为-![]() <d<-3, (2) 在S1,S2,…,S12中,S6最大.
<d<-3, (2) 在S1,S2,…,S12中,S6最大.
解析:
依题意有: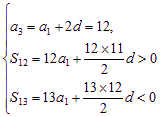
解之得公差d的取值范围为-![]() <d<-3.
<d<-3.
(2)解法一: 由d<0可知a1>a2>a3>…>a12>a13,因此,在S1,S2,…,S12中Sk为最大值的条件为: ak≥0且ak+1<0,即![]()
∵a3=12,∴![]() ,∵d<0,∴2-
,∵d<0,∴2-![]() <k≤3-
<k≤3-![]()
∵-![]() <d<-3,∴
<d<-3,∴![]() <-
<-![]() <4,得5
<4,得5![]() 5<k<7.
5<k<7.
因为k是正整数,所以k=6,即在S1,S2,…,S12中,S6最大.
解法二: 由d<0得a1>a2>…>a12>a13,
若在1≤k≤12中有自然数k,使得ak≥0,且ak+1<0,
则Sk是S1,S2,…,S12中的最大值.
由等差数列性质得,当m、n、p、q∈N*,且m+n=p+q时,am+an=ap+aq. 所以有2a7=a1+a13=![]() S13<0,
S13<0,
∴a7<0,a7+a6=a1+a12=![]() S12>0,∴a6≥-a7>0,
S12>0,∴a6≥-a7>0,
故在S1,S2,…,S12中S6最大.
解法三: 依题意得:![]()
![]() 最小时,Sn最大;
最小时,Sn最大;
∵-![]() <d<-3,∴6<
<d<-3,∴6<![]() (5-
(5-![]() )<6.5.
)<6.5.
从而,在正整数中,当n=6时,[n-![]() (5-
(5-![]() )]2最小,所以S6最大.
)]2最小,所以S6最大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目