题目内容
(2012•马鞍山二模)下面四个命题:
①命题“?x∈R,使得x2+x+l<0”的否定是真命题;
②一组数据18,21,19,a,22的平均数是20,那么这组数据的方差是2;
③已知直线l1:a2x-y+6=0与l2:4x-(a-3)y+9=0,则l1⊥l2的必要条件是a=-1:
④函数f(x)=|lgx|-(
)x有两个零点x1、x2,则一定有0<x1x2<1.
其中真命题是
①命题“?x∈R,使得x2+x+l<0”的否定是真命题;
②一组数据18,21,19,a,22的平均数是20,那么这组数据的方差是2;
③已知直线l1:a2x-y+6=0与l2:4x-(a-3)y+9=0,则l1⊥l2的必要条件是a=-1:
④函数f(x)=|lgx|-(
| 1 | 2 |
其中真命题是
①②④
①②④
(写出所有真命题的序号).分析:①根据命题“?x∈R,使得x2+x+l<0”是假命题,其否定为真命题,从而得到答案.
②先由平均数的公式计算出a的值,再根据方差公式计算.
③根据l1⊥l2 ,斜率之积等于-1可得a2×
=-1,由此求得a的值.
④先将f(x)=|lgx|-(
)x有两个零点转化为y=|lgx|与y=2-x有两个交点,然后在同一坐标系中画出两函数的图象得到零点在(0,1)和(1,+∞)内,即可得到-2-x1=lgx1和2-x2=lg x2,然后两式相加即可求得x1x2的范围.
②先由平均数的公式计算出a的值,再根据方差公式计算.
③根据l1⊥l2 ,斜率之积等于-1可得a2×
| 4 |
| a-3 |
④先将f(x)=|lgx|-(
| 1 |
| 2 |
解答:解:①∵命题“?x∈R,使得x2+x+l<0”是假命题
∴否定命题真命题;正确;
②:a=5×20-1(8+21+19+22)=20,
s2=
[(18-20)2+(21-20)2+(19-20)2+(20-20)2+(22-20)2]=2.
③∵l1⊥l2 ,∴a2×
=-1,4a2+a-3=0,解得 a=3或-1.故③不正确;
④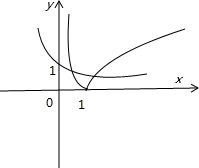 :f(x)=|lgx|-(
:f(x)=|lgx|-(
)x有两个零点x1,x2
即y=|lgx|与y=2-x有两个交点
由题意x>0,分别画y=2-x和y=|lgx|的图象
发现在(0,1)和(1,+∞)有两个交点
不妨设 x1在(0,1)里 x2在(1,+∞)里
那么 在(0,1)上有 2-x1=-lgx1,即-2-x1=lgx1…①
在(1,+∞)有2-x2=lg x2…②
①②相加有2-x2-2-x1=lgx1x2
∵x2>x1,∴2-x2<2-x1 即2-x2-2-x1<0
∴lgx1x2<0
∴0<x1x2<1.正确.
故答案为:①②④.
∴否定命题真命题;正确;
②:a=5×20-1(8+21+19+22)=20,
s2=
| 1 |
| 5 |
③∵l1⊥l2 ,∴a2×
| 4 |
| a-3 |
④
 :f(x)=|lgx|-(
:f(x)=|lgx|-(| 1 |
| 2 |
即y=|lgx|与y=2-x有两个交点
由题意x>0,分别画y=2-x和y=|lgx|的图象
发现在(0,1)和(1,+∞)有两个交点
不妨设 x1在(0,1)里 x2在(1,+∞)里
那么 在(0,1)上有 2-x1=-lgx1,即-2-x1=lgx1…①
在(1,+∞)有2-x2=lg x2…②
①②相加有2-x2-2-x1=lgx1x2
∵x2>x1,∴2-x2<2-x1 即2-x2-2-x1<0
∴lgx1x2<0
∴0<x1x2<1.正确.
故答案为:①②④.
点评:考查命题、统计、逻辑、函数零点、指对数函数性质等,较难题.

练习册系列答案
相关题目