题目内容
对于实数a,b,定义运算“*”:a*b=
,设f(x)=(2x-1)*(x-1),且关于x的方程为f(x)=m(m∈R)恰有三个互不相等的实数根x1,x2,x3,则m的取值范围是
|
(0,
)
| 1 |
| 4 |
(0,
)
.| 1 |
| 4 |
分析:根据题意确定函数的解析式为 f(x)=
,画出函数的图象从图象上观察当关于x的方程为f(x)=m(m∈R)恰有三个互不相等的实数根时m的取值范围.
|
解答:解: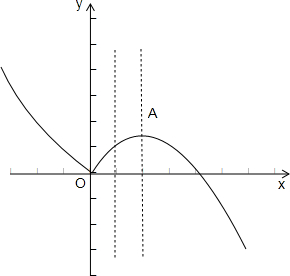 由 2x-1≤x-1 可得 x≤0,由 2x-1>x-1 可得 x>0.
由 2x-1≤x-1 可得 x≤0,由 2x-1>x-1 可得 x>0.
∴根据题意得f(x)=
.
即 f(x)=
,
画出函数的图象,从图象上观察当关于x的方程为f(x)=m(m∈R)恰有三个互不相等的实数根时,
函数的图象和直线y=m有三个不同的交点.
再根据函数的极大值为f(
)=
,
可得m的取值范围是(0,
),
故答案为 (0,
).
 由 2x-1≤x-1 可得 x≤0,由 2x-1>x-1 可得 x>0.
由 2x-1≤x-1 可得 x≤0,由 2x-1>x-1 可得 x>0.∴根据题意得f(x)=
|
即 f(x)=
|
画出函数的图象,从图象上观察当关于x的方程为f(x)=m(m∈R)恰有三个互不相等的实数根时,
函数的图象和直线y=m有三个不同的交点.
再根据函数的极大值为f(
| 1 |
| 2 |
| 1 |
| 4 |
可得m的取值范围是(0,
| 1 |
| 4 |
故答案为 (0,
| 1 |
| 4 |
点评:本题主要考查函数的零点的定义,函数的零点与方程的根的关系,体现了转化、数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
对于实数a和b,定义运算“*”:a*b=
设f(x)=(2x-1)*(x-1),且关于x的方程为f(x)=m(m∈R)恰有三个互不相等的实数根x1,x2,x3,则x1•x2•x3的取值范围是( )
|
A、(-
| ||
B、(-
| ||
C、(0,
| ||
D、(0,
|