Question

对于实数a和b，定义运算“*”：a*b=

-a2+2ab-1，a≤b b2-ab，a＞b.

设f（x）=（2x-1）*（x-1），且关于x的方程为f（x）=m（m∈R）恰有三个互不相等的实数根x₁，x₂，x₃，则x₁•x₂•x₃的取值范围是（　　）

• A、(-

  1

  32

  ，0)
• B、(-

  1

  16

  ，0)
• C、(0，

  1

  32

  )
• D、(0，

  1

  16

  )

Answer 1

分析：由新定义，可以求出函数的解析式，进而求出x的方程为f（x）=m（m∈R）恰有三个互不相等的实数根时，实数m的取值范围，及三个实根之间的关系，进而求出x₁•x₂•x₃的取值范围．

解答：解：由2x-1≤x-1，得x≤0，此时f（x）=（2x-1）*（x-1）=-（2x-1）²+2（2x-1）（x-1）-1=-2x，
由2x-1＞x-1，得x＞0，此时f（x）=（2x-1）*（x-1）=（x-1）²-（2x-1）（x-1）=-x²+x，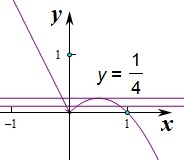
∴f（x）=（2x-1）*（x-1）=

-2x，x≤0 -x2+x，x＞0

，
作出函数的图象可得，
要使方程f（x）=m（m∈R）恰有三个互不相等的实数根x₁，x₂，x₃，不妨设x₁＜x₂＜x₃，
则0＜x₂＜

1

2

＜x₃＜1，且x₂和x₃，关于x=

1

2

对称，
∴x₂+x₃=2×

1

2

=1．则x₂+x₃≥2

x2x3

，0＜x₂x₃＜

1

4

，等号取不到．
当-2x=

1

4

时，解得x=-

1

8

，
∴-

1

8

＜x₁＜0，
∵0＜x₂x₃≤

1

4

，
∴-

1

32

＜x₁•x₂•x₃＜0，
即x₁•x₂•x₃的取值范围是(-

1

32

，0)，
故选：A．

点评：本题考查根的存在性及根的个数判断，根据已知新定义，求出函数的解析式，并分析出函数图象是解答的关键．