题目内容
(2012•福建)对于实数a和b,定义运算“﹡”:a*b=
设f(x)=(2x-1)﹡(x-1),且关于x的方程为f(x)=m(m∈R)恰有三个互不相等的实数根x1,x2,x3,则x1x2x3的取值范围是
|
(
,0)
1-
| ||
| 16 |
(
,0)
.1-
| ||
| 16 |
分析:根据所给的新定义,写出函数的分段形式的解析式,画出函数的图象,在图象上可以看出当直线与函数的图象有三个不同的交点时m的取值,根据一元二次方程的根与系数之间的关系,写出两个根的积和第三个根,表示出三个根之积,根据导数判断出函数的单调性,求出关于m的函数的值域,得到结果.
解答: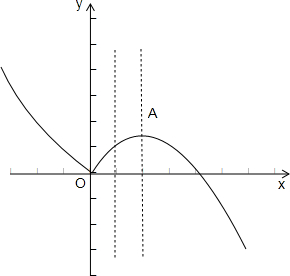 解:∵2x-1≤x-1时,有x≤0,
解:∵2x-1≤x-1时,有x≤0,
∴根据题意得f(x)=
即f(x)=
画出函数的图象从图象上观察当关于x的方程为f(x)=m(m∈R)恰有三个互不相等的实数根时,m的取值范围是(0,
),
当-x2+x=m时,有x1x2=m,
当2x2-x=m时,由于直线与抛物线的交点在y轴的左边,得到x3=
,
∴x1x2x3=m(
)=
,m∈(0,
)
令y=
,
则y′=
(1-
-
),又h(m)=
+
在m∈(0,
)上是增函数,故有h(m)>h(0)=1
∴y′=
(1-
-
)<0在m∈(0,
)上成立,
∴函数y=
在这个区间(0,
)上是一个减函数,
∴函数的值域是(f(
),f(0)),即(
,0)
故答案为:(
,0)
 解:∵2x-1≤x-1时,有x≤0,
解:∵2x-1≤x-1时,有x≤0,∴根据题意得f(x)=
|
即f(x)=
|
画出函数的图象从图象上观察当关于x的方程为f(x)=m(m∈R)恰有三个互不相等的实数根时,m的取值范围是(0,
| 1 |
| 4 |
当-x2+x=m时,有x1x2=m,
当2x2-x=m时,由于直线与抛物线的交点在y轴的左边,得到x3=
1-
| ||
| 4 |
∴x1x2x3=m(
1-
| ||
| 4 |
m-m
| ||
| 4 |
| 1 |
| 4 |
令y=
m-m
| ||
| 4 |
则y′=
| 1 |
| 4 |
| 1+8m |
| 4m | ||
|
| 1+8m? |
| 4m | ||
|
| 1 |
| 4 |
∴y′=
| 1 |
| 4 |
| 1+8m |
| 4m | ||
|
| 1 |
| 4 |
∴函数y=
m-m
| ||
| 4 |
| 1 |
| 4 |
∴函数的值域是(f(
| 1 |
| 4 |
1-
| ||
| 16 |
故答案为:(
1-
| ||
| 16 |
点评:本题考查分段函数的图象,考查新定义问题,这种问题解决的关键是根据新定义写出符合条件的解析式,本题是一个综合问题,涉及到导数判断函数的单调性,本题是一个中档题目.

练习册系列答案
相关题目
