题目内容
(2013•婺城区模拟)设不等式组
表示的平面区域为D.若圆C:(x+1)2+(y+1)2=r2(r>0)不经过区域D上的点,则r的取值范围是( )
|
分析:作出题中不等式组表示的平面区域,得到如图的△MNP及其内部,而圆C表示以(-1,-1)为圆心且半径为r的圆.观察图形,可得半径r<CM或r>CP时,圆C不经过区域D上的点,由此结合平面内两点之间的距离公式,即可得到r的取值范围.
解答:解: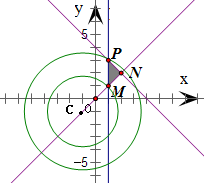 作出不等式组
作出不等式组
表示的平面区域,
得到如图的△MNP及其内部,其中M(1,1),N(2,2),P(1,3)
∵圆C:(x+1)2+(y+1)2=r2(r>0),
表示以C(-1,-1)为圆心,半径为r的圆
∴由图可得,当半径满足r<CM或r>CP时,圆C不经过区域D上的点,
∵CM=
=2
,CP=
=2
∴当0<r<2
或r>2
时,圆C不经过区域D上的点
故选:D
 作出不等式组
作出不等式组
|
得到如图的△MNP及其内部,其中M(1,1),N(2,2),P(1,3)
∵圆C:(x+1)2+(y+1)2=r2(r>0),
表示以C(-1,-1)为圆心,半径为r的圆
∴由图可得,当半径满足r<CM或r>CP时,圆C不经过区域D上的点,
∵CM=
| (1+1)2+(1+1)2 |
| 2 |
| (1+1)2+(3+1)2 |
| 5 |
∴当0<r<2
| 2 |
| 5 |
故选:D
点评:本题给出动圆不经过已知不等式组表示的平面区域,求半径r的取值范围.着重考查了圆的标准方程、平面内两点间的距离公式、二元一次不等式组表示的平面区域等知识,属于中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 (2013•婺城区模拟)已知点P是双曲线C:
(2013•婺城区模拟)已知点P是双曲线C: