题目内容
设函数y=f(x)的定义域为［0，1］，求下列函数的定义域.
（1）y=f(3x); (2)y=f(
);(3)y=f(
; (4)y=f(x+a)+f(x-a).
（1）［0, 
］（2）［1，+∞)（3）
（４）当0≤a≤
时，定义域为［a，1-a］；当-≤a≤0时，定义域为［-a，1+a］
解析:
：（1）0≤3x≤1,故0≤x≤,y=f(3x)的定义域为［0, ］.
（2）仿（1）解得定义域为［1，+∞).
（3）由条件，y的定义域是f
与
定义域的交集.
列出不等式组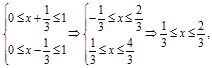
故y=f
的定义域为.
（４）由条件得
讨论：
①当
即0≤a≤时，定义域为［a,1-a］;
②当
即-≤a≤0时，定义域为［-a,1+a］.
综上所述：当0≤a≤时，定义域为［a，1-a］；当-≤a≤0时，定义域为［-a，1+a］.
练习册系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
，1)，则y=f-1(x)的图象必过点( )
,1) B.(1,
) C.(1,0) D.(0,1)
)的值；
.(2a1－1)·(2a2－1)…(2an－1)对于一切n∈N*均成立？若存在，求出M的范围；若不存在，请说明理由.