题目内容
函数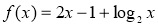
的零点所在的一个区间是( )
A.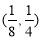
B.
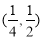C.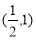
D.(1,2)
C
【解析】
试题分析：通过计算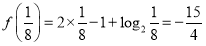
；
；
；
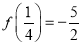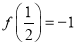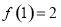，因为
，故答案选C．
考点：1．函数零点的存在性定理；2．对函数运算．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
天天向上一本好卷系列答案小学生10分钟应用题系列答案题目内容
函数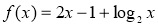的零点所在的一个区间是( )
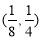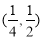A. B. C.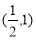 D.(1,2)
C
【解析】
试题分析：通过计算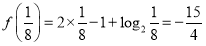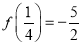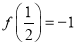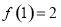；；；，因为，故答案选C．
考点：1．函数零点的存在性定理；2．对函数运算．
天天向上一本好卷系列答案小学生10分钟应用题系列答案
