题目内容
△ABC中,三内角A、B、C所对边的长分别为a、b、c,已知B=60°,不等式-x2+6x-8>0的解集为{x|a<x<c},则b= .
【答案】分析:先解一元二次不等式可求出a,c的值,结合已知B=60°,然后利用余弦定理可得,b2=a2+c2-2acc×os60°可求b
解答:解:∵不等式-x2+6x-8>0的解集为{x|2<x<4}
∴a=2,c=4
B=60°
根据余弦定理可得,b2=a2+c2-2acc×os60°=12
b=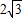
故答案为: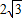
点评:本题以一元二次不等式的解集为切入点,考查了余弦定理的简单运用,属于知识的简单综合.
解答:解:∵不等式-x2+6x-8>0的解集为{x|2<x<4}
∴a=2,c=4
B=60°
根据余弦定理可得,b2=a2+c2-2acc×os60°=12
b=
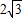
故答案为:
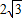
点评:本题以一元二次不等式的解集为切入点,考查了余弦定理的简单运用,属于知识的简单综合.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目