题目内容
【题目】在直角坐标标系xoy中,已知曲线 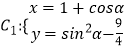 (α为参数,α∈R),在以原点O为极点,x轴非负半轴为极轴的极坐标系中(取相同的长度单位),曲线
(α为参数,α∈R),在以原点O为极点,x轴非负半轴为极轴的极坐标系中(取相同的长度单位),曲线 ![]() =
= ![]() ,曲线C3:ρ=2cosθ. (Ⅰ)求曲线C1与C2的交点M的直角坐标;
,曲线C3:ρ=2cosθ. (Ⅰ)求曲线C1与C2的交点M的直角坐标;
(Ⅱ)设A,B分别为曲线C2 , C3上的动点,求|AB|的最小值.
【答案】解:(Ⅰ)曲线 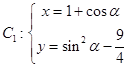 (α为参数,α∈R),消去参数α, 得:y=﹣
(α为参数,α∈R),消去参数α, 得:y=﹣ ![]() ﹣(x﹣1)2 , x∈[0,2],①
﹣(x﹣1)2 , x∈[0,2],①
∵曲线 ![]() =
= ![]() ,∴ρcosθ+ρsinθ+1=0,
,∴ρcosθ+ρsinθ+1=0,
∴曲线C2:x+y+1=0,②,
联立①②,消去y可得:4x2﹣12x+5=0,解得x= ![]() 或x=
或x= ![]() (舍去),
(舍去),
∴M( ![]() ).
).
(Ⅱ)曲线C3:ρ=2cosθ,即ρ2=2ρcosθ,
∴曲线C3:(x﹣1)2+y2=1,是以C3(1,0)为圆心,半径r=1的圆
圆心C3到直线x+y+1=0的距离为d= ![]() ,
,
∴|AB|的最小值为 ![]() -1
-1
【解析】(Ⅰ)求出曲线C1的普通方程和曲线C2的直角坐标方程,联立方程组能求出曲线C1与C2的交点M的直角坐标.(Ⅱ)曲线C3是以C(1,0)为圆心,半径r=1的圆,求出圆心C3到直线x+y+1=0的距离d,由此能求出|AB|的最小值.

练习册系列答案
相关题目