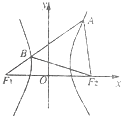
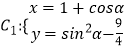题目内容
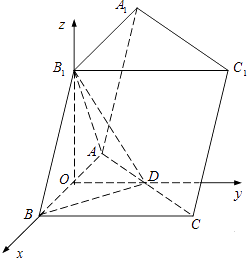
【题目】如图,在三棱柱ABC﹣A1B1C1中,B1B=B1A=AB=BC,∠B1BC=90°,D为AC的中点,AB⊥B1D. 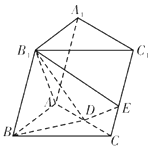
(1)求证:平面ABB1A1⊥平面ABC;
(2)在线段CC1(不含端点)上,是否存在点E,使得二面角E﹣B1D﹣B的余弦值为 ![]() ?若存在,求出
?若存在,求出 ![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
【答案】
(1)证明:取AB中点为O,连接OD,OB1.
因为B1B=B1A,所以OB1⊥AB.
又AB⊥B1D,OB1∩B1D=B1,所以AB⊥平面B1OD,
因为OD平面B1OD,所以AB⊥OD.
由已知,BC⊥BB1,又OD∥BC,
所以OD⊥BB1,因为AB∩BB1=B,
所以OD⊥平面ABB1A1.
又OD平面ABC,所以平面ABC⊥平面ABB1A1
(2)解:由(1)知,OB,OD,OB1两两垂直.
以O为坐标原点, ![]() 的方向为x轴的方向,|
的方向为x轴的方向,| ![]() |为单位长度1,建立如图所示的空间直角坐标系O﹣xyz.
|为单位长度1,建立如图所示的空间直角坐标系O﹣xyz.
由题设知B1(0,0, ![]() ),B(1,0,0),D(0,1,0),A(﹣1,0,0),C(1,2,0),C1(0,2,
),B(1,0,0),D(0,1,0),A(﹣1,0,0),C(1,2,0),C1(0,2, ![]() ).
).
∴ ![]() =(0,1,﹣
=(0,1,﹣ ![]() ),
), ![]() =(1,0,﹣
=(1,0,﹣ ![]() ),
),
设 ![]() =λ
=λ ![]() ,(0<λ<1),则
,(0<λ<1),则 ![]() =
= ![]() =(1﹣λ,2,
=(1﹣λ,2, ![]() ),
),
设平面BB1D的法向量 ![]() =(x,y,z),
=(x,y,z),
则 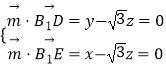 ,取z=1,得
,取z=1,得 ![]() =(
=( ![]() ),
),
设平面B1DE的法向量 ![]() =(x,y,z),
=(x,y,z),
则 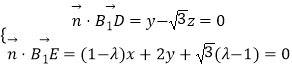 ,取z=1,得
,取z=1,得 ![]() =(
=( ![]() ,
, ![]() ,1),
,1),
∵二面角E﹣B1D﹣B的余弦值为 ![]() ,
,
∴﹣|cos< ![]() >|=﹣
>|=﹣ ![]() =﹣
=﹣ 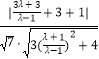 =﹣
=﹣ ![]() ,
,
解得λ= ![]() ,
,
∴在线段CC1(不含端点)上,存在点E,使得二面角E﹣B1D﹣B的余弦值为 ![]() ,且
,且 ![]() =
= ![]() .
.
【解析】(1)取AB中点为O,连接OD,OB1 . 推导出OB1⊥AB,AB⊥B1D,从而AB⊥平面B1OD,进而AB⊥OD.再求出BC⊥BB1 , OD⊥BB1 , 从而OD⊥平面ABB1A1 . 由此能证明平面ABC⊥平面ABB1A1 . (2)以O为坐标原点, ![]() 的方向为x轴的方向,|
的方向为x轴的方向,| ![]() |为单位长度1,建立如图所示的空间直角坐标系O﹣xyz.利用向量法求出在线段CC1(不含端点)上,存在点E,使得二面角E﹣B1D﹣B的余弦值为
|为单位长度1,建立如图所示的空间直角坐标系O﹣xyz.利用向量法求出在线段CC1(不含端点)上,存在点E,使得二面角E﹣B1D﹣B的余弦值为 ![]() ,且
,且 ![]() =
= ![]() .
.
【考点精析】认真审题,首先需要了解平面与平面垂直的判定(一个平面过另一个平面的垂线,则这两个平面垂直).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案