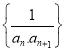题目内容
【题目】设集合![]()
(1)当A中元素个数为1时,求:a和A;
(2)当A中元素个数至少为1时,求:a的取值范围;
(3)求:A中各元素之和.
【答案】(1)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 时,A中元素之和为
时,A中元素之和为![]() ;当
;当![]() 且
且![]() 时,A中元素之和为
时,A中元素之和为![]() ;当
;当![]() 时,A中元素之和为
时,A中元素之和为![]() ;当
;当![]() 时,A中无元素;
时,A中无元素;
【解析】
集合中元素的个数就是方程![]() 的解的个数。(1)当A中元素个数为1时,方程一个解,要考虑二次项系数是否为0,不等于0时,按一元二次方程处理;(2)当A中元素个数至少为1时,方程至少一个解,要考虑二次项系数是否为0,不等于0时,按一元二次方程处理;(3)求A中各元素之和,就是求方程
的解的个数。(1)当A中元素个数为1时,方程一个解,要考虑二次项系数是否为0,不等于0时,按一元二次方程处理;(2)当A中元素个数至少为1时,方程至少一个解,要考虑二次项系数是否为0,不等于0时,按一元二次方程处理;(3)求A中各元素之和,就是求方程![]() 解的和。要考虑二次项系数是否为0,等于0时,可以求根。不等于0时,按一元二次方程处理,要讨论是否有解。
解的和。要考虑二次项系数是否为0,等于0时,可以求根。不等于0时,按一元二次方程处理,要讨论是否有解。
(1) 当A中元素个数为1时,集合![]() 中的方程
中的方程![]() 只有一个解。当
只有一个解。当![]() 时,方程变为
时,方程变为![]() ,方程只有一个解
,方程只有一个解![]() ,符合题意,此时
,符合题意,此时![]() ;当
;当![]() 时,
时,![]() ,所以,
,所以,![]() ,此时,
,此时,![]() ; 综上,当
; 综上,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 。
。
(2) 当A中元素个数至少为1时,集合![]() 中的方程
中的方程![]() 至少有一个解。由(1)知,
至少有一个解。由(1)知,![]() 符合题意;当
符合题意;当![]() 时,
时,![]() ,解得
,解得![]() ,所以
,所以![]() 且
且![]() 。综上,a的取值范围为
。综上,a的取值范围为![]() 。
。
(3)由(1)知,当![]() 时,集合A中元素之和为
时,集合A中元素之和为![]() ,当
,当![]() 时,A中元素之和为
时,A中元素之和为![]() ;由(2)知,当
;由(2)知,当![]() 且
且![]() 时,方程
时,方程![]() 有两个根,由韦达定理可得A中元素之和为
有两个根,由韦达定理可得A中元素之和为![]() ;当
;当![]() 时,
时,![]() ,此时,方程
,此时,方程![]() 无解。综上所述,当
无解。综上所述,当![]() 时,A中元素之和为
时,A中元素之和为![]() ;当
;当![]() 且
且![]() 时,A中元素之和为
时,A中元素之和为![]() ;当
;当![]() 时,A中元素之和为
时,A中元素之和为![]() ;当
;当![]() 时,A中无元素。
时,A中无元素。

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目