题目内容
 (1)画出函数f(x)=|x|(x-4)的图象并指出单调区间;
(1)画出函数f(x)=|x|(x-4)的图象并指出单调区间;(2)利用图象讨论:关于x方程f(x)=a(a为常数)解的个数?
分析:(1)利用零点分段法,将函数的解析式化为分段函数的形式,进而根据分段函数分段画的原则,得到函数图象,进而根据图象上升对应函数的单调递增区间,图象下降对应函数的单调递减区间,得到答案.
(2)结合(1)中函数的图象,结合函数f(x)=|x|(x-4)的图象与y=a的交点个数,分类讨论可得答案.
(2)结合(1)中函数的图象,结合函数f(x)=|x|(x-4)的图象与y=a的交点个数,分类讨论可得答案.
解答:解:(1)∵f(x)=|x|(x-4)=
其图象如下图所示:
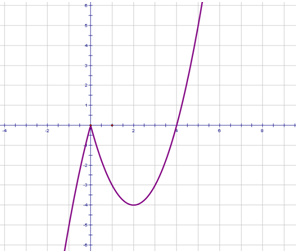
由图可知函数f(x)的单调递增区间为:(-∞,0],[2,+∞)
单调递减区间为:[0,2]
(2)由图可知:
当a<-4或a>0时,f(x)=a有1个解
当a=-4或a=0时,f(x)=a有2个解
当-4<a<0时,f(x)=a有3个解
|
其图象如下图所示:

由图可知函数f(x)的单调递增区间为:(-∞,0],[2,+∞)
单调递减区间为:[0,2]
(2)由图可知:
当a<-4或a>0时,f(x)=a有1个解
当a=-4或a=0时,f(x)=a有2个解
当-4<a<0时,f(x)=a有3个解
点评:本题考查的知识点是函数图象的作法,根的存在性及根的个数,根据分段函数分段画的原则,得到函数图象,是解答的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 已知函数
已知函数 已知函数
已知函数