题目内容
已知函数f(x)=2|x-1|-3|x|.
(1)画出函数f(x)的图象;
(2)根据图象求函数f(x)=2|x-1|-3|x|的最大值;
(3)根据图象解不等式f(x)<0.
(1)画出函数f(x)的图象;
(2)根据图象求函数f(x)=2|x-1|-3|x|的最大值;
(3)根据图象解不等式f(x)<0.
分析:(1)根据函数f(x)=2|x-1|-3|x|=
,画出函数f(x)的图象.
(2)根据图象可得,当x=0时,函数f(x)=2|x-1|-3|x|取得最大值为2.
(3)根据图象,数形结合可得不等式f(x)<0的解集.
|
(2)根据图象可得,当x=0时,函数f(x)=2|x-1|-3|x|取得最大值为2.
(3)根据图象,数形结合可得不等式f(x)<0的解集.
解答: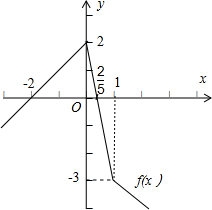 解:(1)由于函数f(x)=2|x-1|-3|x|=
解:(1)由于函数f(x)=2|x-1|-3|x|=
,
画出函数f(x)的图象,如图所示:
(2)根据图象可得,当x=0时,
函数f(x)=2|x-1|-3|x|取得最大值为2.
(3)根据图象可得,不等式f(x)<0的解集为
(-∞,-2)∪(
,+∞).
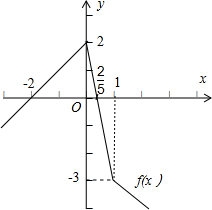 解:(1)由于函数f(x)=2|x-1|-3|x|=
解:(1)由于函数f(x)=2|x-1|-3|x|=
|
画出函数f(x)的图象,如图所示:
(2)根据图象可得,当x=0时,
函数f(x)=2|x-1|-3|x|取得最大值为2.
(3)根据图象可得,不等式f(x)<0的解集为
(-∞,-2)∪(
| 2 |
| 5 |
点评:本题主要考查带有绝对值的函数,函数图象的作法,结合图象解绝对值不等式,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目