题目内容

若函数f（x）=2013sin（?x+θ）满足对任意的x都有f（x）=f（2-x），则2014cos（?+θ）=______．
∵任意的x都有f（x）=f（2-x），
∴函数f（x）=2013sin（?x+θ）的图象关于直线x=1对称，
可得f（1）=2013sin（?+θ）=1或f（1）=2013sin（?+θ）=-1
因此，?+θ=
π
2
+kπ（k∈Z），可得cos（
π
2
+kπ）=±cos
π
2
=0
由此可得：2014cos（ ?+θ）=2014cos（
π
2
+kπ）=0
故答案为：0
练习册系列答案
相关题目
将函数y=2sin(3x+
π
6
)（x∈R）的图象上所有的点向左平行移动
π
4
个单位长度，再把图象上各点的横坐标扩大到原来的2倍（纵坐标不变），则所得到的图象的解析式为（　　）
A．y=2sin(6x+
11
12
π)		B．y=2sin(
3
2
x+
11
12
π)
C．y=2sin(6x+
5
12
π)		D．y=2sin(
3
2
x+
5
12
π)
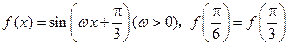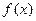已知，且在区间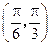有最小值，无最大值，则＝__________．
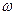函数y=sinx（
π
6
≤x≤
2
3
π）的值域为（　　）
A．[
1
2
，1]		B．[-1，1]C．[
1
2
，
3
2
]		D．[
3
2
，1]
若α，β都是第一象限角，且α＜β，那么（　　）
A．sinα＞sinβB．sinβ＞sinα
C．sinα≥sinβD．sinα与sinβ的大小不定
函数y=tan(2x-
π
4
)的周期是（　　）
A．πB．
π
2
C．
π
4
D．2π
函 f（x）=Asin（ωx+φ）（A＞0，ω＞0，0≤φ＜2π）在R上的部分图象如图所示，则 f（x）=______．
如图为f（x）=Asin（ωx+ϕ）（A＞0，?＞0，ϕ∈（-π，0））的图象的一段，
（Ⅰ）求其解析式．
（Ⅱ）将f（x）图象上所有的点纵坐标不变，横坐标放大到原来的2倍，然后再将新的图象向左平移
π
2
个单位，得到函数g（x）的图象，求函数g（x）在x∈[0，
π
2
]的值域．
已知f（x）=sin(ωx+
π
3
)（ω＞0），f（
π
6
）=f（
π
3
），且f（x）在区间(
π
6
，
π
3
)上有最小值，无最大值，则ω=______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网