题目内容
【题目】函数f(x)=loga(x+1),(a>0,a≠1)的图象经过点(﹣ ![]() ,﹣2),图象上有三个点A,B,C,它们的横坐标依次为t﹣1,t,t+1,(t≥1),记三角形ABC的面积为S(t),
,﹣2),图象上有三个点A,B,C,它们的横坐标依次为t﹣1,t,t+1,(t≥1),记三角形ABC的面积为S(t), 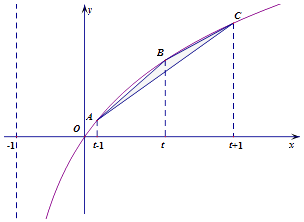
(1)求f(x)的表达式;
(2)求S(1);
(3)是否存在正整数m,使得对于一切不小于1的t,都有S(t)<m,若存在求的最小值,若不存在,请说明理由.
【答案】
(1)解:∵f(x)=loga(x+1),(a>0,a≠1)的图象经过点(﹣ ![]() ,﹣2),
,﹣2),
∴﹣2=loga(﹣ ![]() +1),∴a=2
+1),∴a=2
∴f(x)=log2x
(2)解:当t=1时,A(0,0),B(1,1),C(2,log23),
∴S(1)= ![]() (xB﹣xA)yB+
(xB﹣xA)yB+ ![]() ({xC﹣xB)(yB+yC)﹣
({xC﹣xB)(yB+yC)﹣ ![]() (xC﹣xA)yC=1﹣log23(3)由图知:S(t)=
(xC﹣xA)yC=1﹣log23(3)由图知:S(t)= ![]() [log2t+log2(t+1)]+
[log2t+log2(t+1)]+ ![]() [log2(t+1)+log2(t+2)]﹣
[log2(t+1)+log2(t+2)]﹣ ![]() [log2t+log2(t+2)}]×2
[log2t+log2(t+2)}]×2
= ![]() log2[{1+
log2[{1+ ![]() ]
]
∵对一切不小于1的t,t(t+2)≥3,0< ![]() ≤
≤ ![]() ,
,
∴1<1+ ![]() ≤
≤ ![]() ,
,
∴0<log2[{1+ ![]() ]≤log2
]≤log2 ![]() ,
,
∴0< ![]() log2[{1+
log2[{1+ ![]() ]≤
]≤ ![]() log2
log2 ![]()
(3)解:要使对一切不小于1的t,S(t)<m均成立,只需m>S(t)max,
∴m> ![]() log2
log2 ![]()
又∵m∈N*,∴m=1
【解析】(1)利用f(x)=loga(x+1),(a>0,a≠1)的图象经过点(﹣ ![]() ,﹣2),求出a,即可求出f(x)的表达式;(2)S(1)=
,﹣2),求出a,即可求出f(x)的表达式;(2)S(1)= ![]() (xB﹣xA)yB+
(xB﹣xA)yB+ ![]() ({xC﹣xB)(yB+yC)﹣
({xC﹣xB)(yB+yC)﹣ ![]() (xC﹣xA)yC , 即可求S(1);(3)要使对一切不小于1的t,S(t)<m均成立,只需m>S(t)max , 即可得出结论.
(xC﹣xA)yC , 即可求S(1);(3)要使对一切不小于1的t,S(t)<m均成立,只需m>S(t)max , 即可得出结论.

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案【题目】已知椭圆C: ![]() 的短轴长为2,离心率为
的短轴长为2,离心率为 ![]() ,设过右焦点的直线l与椭圆C交于不同的两点A,B,过A,B作直线x=2的垂线AP,BQ,垂足分别为P,Q.记
,设过右焦点的直线l与椭圆C交于不同的两点A,B,过A,B作直线x=2的垂线AP,BQ,垂足分别为P,Q.记 ![]() ,若直线l的斜率k≥
,若直线l的斜率k≥ ![]() ,则λ的取值范围为 .
,则λ的取值范围为 .
【题目】随着生活水平的提高,人们对空气质量的要求越来越高,某机构为了解公众对“车辆限行”的态度,随机抽查![]() 人,并将调查情况进行整理后制成下表:
人,并将调查情况进行整理后制成下表:
年龄(岁) |
|
|
|
|
|
频数 |
|
|
|
|
|
赞成人数 |
|
|
|
|
|
(1)完成被调查人员年龄的频率分布直方图,并求被调査人员中持赞成态度人员的平均年龄约为多少岁?
(2)若从年龄在![]() 的被调查人员中各随机选取
的被调查人员中各随机选取![]() 人进行调查.请写出所有的基本亊件,并求选取
人进行调查.请写出所有的基本亊件,并求选取![]() 人中恰有
人中恰有![]() 人持不赞成态度的概率.
人持不赞成态度的概率.
