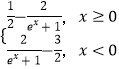题目内容
【题目】某养鸡场是一面靠墙，三面用铁丝网围成的矩形场地，如果铁丝网长40m，那么围成的场地面积最大为多少？
【答案】解：设围成的矩形场地的长为am，宽为bm， 由题意可得a+2b=40，
则围成的场地面积设为S，
即有S=ab= 
a2b≤ （ 
）2
= （ 
）2=200．
当且仅当a=2b，即a=20m，b=10m时，取得最大值200m2 ．
则围成的场地面积最大为200m2 ． 
【解析】设围成的矩形场地的长为am，宽为bm，由题意可得a+2b=40，则矩形的面积S=ab，由基本不等式即可得到所求最大值．
【考点精析】解答此题的关键在于理解基本不等式在最值问题中的应用的相关知识，掌握用基本不等式求最值时（积定和最小，和定积最大），要注意满足三个条件“一正、二定、三相等”．
练习册系列答案
相关题目
